-- Author: Juan Mena Parra, 2012-04-29
thickness and 
adhesive is used to pick up the eight lines. The spacing between (borders of) adjacent lines is (ideally) uniform along the stripline and approximately 37.5 mil (66.5 mil between centers). So far, striplines with two different lengths have been produced: 27.5'' and 37.5''. In this wiki we will characterize the lines 1 and 8 of the McG-SL-w03_007 stripline, which is 27.5'' long (including copper ends).
Figure 1
In order to characterize the stripline we will treat each line as a transmission line, that is, we will assume a distributed element model in which the parameters of the line (RLGC) are distributed continuously throughout its material. Now, in practice, the striplines will be used at very low temperatures (about 250mK to 4 K), and in that case the resistance of the NbTi wires is (almost) zero. In general, it is safe to assume for a transmission line that the losses due to the dielectric material (Kapton film in this case) are low so the conductance is also (almost) zero. This means that when used at low temperatures the lines behave as lossless transmission lines and they are completely characterized by their inductance L and capacitance C . Determine L and C for a lossless transmission line is relatively easy. However, in practice it will be very hard to perform measurements on the stripline while keeping it at low temperature, do to the challenges of having to inject and recover the signals through feedthroughs and other wiring. So we choose to characterize the striplines at room temperature.
If you have seen a stripline you may ask why we do not just assume that each line behaves as a parallel plate transmission line in which case, as first approximation, L and C can be determined from 
and 
where 
is the length of the line, 
is the wire width and 
is the thickness of the Kapton film, 
its permittivity and 
its permeability. Well, the reason is that these equations not only fail in this case, but they fail miserably, as we will see.
This basically means that we will have to measure L and C at room temperature. However we have the additional problem that at room temperature the lines behave as a VERY lossy transmission line because the resistance R of the NbTi wire is about 
(measured with multimeter). So we will treat each line as a general lossy transmission line. Notice that with this approach we are assuming that the values of L and C that we measure at room temperature will not change (much) as the temperature is decreased to 4 K. However, this assumption is not that crazy: even if we assume a distributed element model for each line without a particular geometry, it makes sense to assume that the parameters of the line depend on its geometry (whatever it is) and maybe on the input so in that case we can expect that these parameters will remain approximately constant as the temperature is decreased (REALLY??).
Figure 2
For a transmission line like the one shown in Figure 2 above with length 
, characteristic impedance 
, load impedance 
, generator impedance 
the general Telegrapher's equations can be written as
%BEGINLATEX%
\begin{eqnarray}
\frac{\partial ^2 V(z)}{\partial z^2} &= \gamma ^2 V(z) \hspace{1in} (1) \nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
\frac{\partial ^2 I(z)}{\partial z^2} &= \gamma ^2 I(z) \hspace{1in} (2) \nonumber
\end{eqnarray}
%ENDLATEX%
The solutions for 
and 
in the frequency domain are
%BEGINLATEX%
\begin{eqnarray}
V(z)= V^+ e^{-\gamma z}+ V^- e^{\gamma z} \hspace{1in} (3)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
I(z)= \frac{1}{Z_0} \left(V^+ e^{-\gamma z}- V^- e^{\gamma z}\right) \hspace{1in} (4)\nonumber
\end{eqnarray}
%ENDLATEX%
where
%BEGINLATEX%
\begin{eqnarray}
\gamma= \sqrt{(R+j \omega L)(G+j \omega C)} \hspace{1in} (5)\nonumber
\end{eqnarray}
%ENDLATEX%
is the propagation constant and
%BEGINLATEX%
\begin{eqnarray}
Z_0= \sqrt{\frac{R+j \omega L}{G+j \omega C}} \hspace{1in} (6)\nonumber
\end{eqnarray}
%ENDLATEX%
is the characteristic impedance. The constants 
, 
are determined by the boundary conditions and are associated with waves traveling in the +z and -z directions respectively. Now, The impedance of the transmission line at a distance z from the load, that is, the load impedance "seen" by a generator placed a distance z from the load is
%BEGINLATEX%
\begin{eqnarray}
Z(z)= \frac{V(z)}{I(z)}=Z_0 \frac{V^+ e^{-\gamma z}+ V^- e^{\gamma z}}{V^+ e^{-\gamma z}- V^- e^{\gamma z}}=Z_0 \frac{1+\Gamma (z)}{1- \Gamma (z)} \hspace{1in} (7) \nonumber
\end{eqnarray}
%ENDLATEX%
where
%BEGINLATEX%
\begin{eqnarray}
\Gamma (z)= \frac{V^-}{V^+} e^{2\gamma z} \hspace{1in} (8)\nonumber
\end{eqnarray}
%ENDLATEX%
is the reflection coefficient, the ratio between in the reflected and incident wave at any point of the transmission line. It is clear from equation (7) that
%BEGINLATEX%
\begin{eqnarray}
\Gamma (z)= \frac{Z(z)-Z_0}{Z(z)+Z_0} \hspace{1in} (9)\nonumber
\end{eqnarray}
%ENDLATEX%
In particular, at the load (z=0)
%BEGINLATEX%
\begin{eqnarray}
\Gamma _L=\frac{V^-}{V^+}= \frac{Z_L-Z_0}{Z_L+Z_0} \hspace{1in} (10)\nonumber
\end{eqnarray}
%ENDLATEX%
So now we can write 
as
%BEGINLATEX%
\begin{eqnarray}
Z(z)=Z_0 \frac{e^{-\gamma z}+ \frac{\displaystyle Z_L-Z_0}{\displaystyle Z_L+Z_0} e^{\gamma z}}{e^{-\gamma z}- \frac{\displaystyle Z_L-Z_0}{\displaystyle Z_L+Z_0} e^{\gamma z}}=Z_0 \frac{ Z_L \left( e^{\gamma z}+e^{\gamma z} \right)- Z_0 \left( e^{\gamma z}-e^{\gamma z} \right)}{Z_0 \left( e^{\gamma z}+e^{\gamma z} \right)- Z_L \left( e^{\gamma z}-e^{\gamma z} \right)}=Z_0 \frac{Z_L - Z_0 tanh(\gamma z)}{Z_0 - Z_L tanh(\gamma z)} \hspace{1in} (11)\nonumber
\end{eqnarray}
%ENDLATEX%
In particular, the input impedance of the transmission line is
%BEGINLATEX%
\begin{eqnarray}
Z_{in}=Z(-l)=Z_0 \frac{Z_L + Z_0 tanh(\gamma l)}{Z_0 + Z_L tanh(\gamma l)} \hspace{1in} (12)\nonumber
\end{eqnarray}
%ENDLATEX%
Recall that 
and 
are complex in general so this equation can be very ugly. There are two special cases: When the load is a short circuit we have
%BEGINLATEX%
\begin{eqnarray}
Z_{in~sc}=Z_0 tanh(\gamma l) \hspace{1in} (13)\nonumber
\end{eqnarray}
%ENDLATEX%
and when the load is an open circuit have
%BEGINLATEX%
\begin{eqnarray}
Z_{in~oc}=\frac{Z_0}{tanh(\gamma l)} \hspace{1in} (14)\nonumber
\end{eqnarray}
%ENDLATEX%
and we have arrived to two very important equations for us
%BEGINLATEX%
\begin{eqnarray}
Z_0=\pm \sqrt{Z_{in~sc}~ Z_{in~oc}} \hspace{1in} (15) \nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
\gamma l=\pm tanh^{-1} \left(\sqrt{\frac{Z_{in~sc}}{Z_{in~oc}}}\right) \hspace{1in} (16)\nonumber
\end{eqnarray}
%ENDLATEX%
We included the 
sign just to remind you that you will obtain two roots, however only one of them will give you a physically acceptable value. For example, the real part of the propagation constant corresponds to the attenuation constant 
and its value cannot be negative (I mean, it can be negative but it would have to be interpreted as the attenuation constant for propagation in -z direction). Similarly, the real part of the characteristic impedance, 
cannot be negative (IS THIS TRUE??.)
Once and are found, the RLGC parameters are determined immediately from equations (5) and (6)
%BEGINLATEX%
\begin{eqnarray}
R=\Re (\gamma Z_0) \hspace{1in} (17)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
L=\frac{\Im (\gamma Z_0)}{\omega} \hspace{1in} (18)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
G=\Re \left( \gamma/Z_0 \right) \hspace{1in} (19)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
C=\frac{\Im (\gamma/Z_0)}{\omega} \hspace{1in} (20)\nonumber
\end{eqnarray}
%ENDLATEX%
where we take 
meaning that the RLGC parameters are calculated per unit length of the transmission line. Now, for this wiki the only things you need to know about Scattering parameters is that the reflection coefficient 
is a measurable parameter and that the parameter 
is just the reflection coefficient at the input of the transmission line. That means that if you connect a transmission line with input impedance 
to a Vector Network Analyzer (here we will use the Agilent E5071C) with reference impedance 
(which is generally 
) and measure then
%BEGINLATEX%
\begin{eqnarray}
S_{11}= \frac{Z_{in}-Z_r}{Z_{in}+Z_r} \hspace{1in} (21)\nonumber
\end{eqnarray}
%ENDLATEX%
or
%BEGINLATEX%
\begin{eqnarray}
Z_{in}= Z_r \frac{1+S_{11}}{1- S_{11}} \hspace{1in} (22) \nonumber
\end{eqnarray}
%ENDLATEX%
Then, in theory, we have solved the problem of characterizing the transmission line. We can measure with with the transmission line terminated in a short-circuit (call this value 
) and find 
from equation (22). With the same procedure but this time with the transmission line terminated in an open-circuit we can measure 
and find 
. Then we can determine and from equations (15) and (16) and finally we can determine the RLGC parameters from equations (17)-(20).
Once the RLGC parameters are determined we can check if our method really works by predicting the value of for an arbitrary load and then comparing with the measured value. In our case we will test our model by measuring with the transmission line terminated with a load . This means that we will have to find expressions for with arbitrary loads. If we substitute from equation (12) into equation (21) obtain
%BEGINLATEX%
\begin{eqnarray}
S_{11}= \frac{Z_0(Z_L-Z_r)+tanh(\gamma)(Z_0 ^2-Z_L Z_r)}{Z_0(Z_L+Z_r)+tanh(\gamma)(Z_0 ^2+Z_L Z_r)} \hspace{1in} (22)\nonumber
\end{eqnarray}
%ENDLATEX%
In the special cases when the load is a short-circuit, open-circuit and (
) we obtain
%BEGINLATEX%
\begin{eqnarray}
S_{11~sc}= \frac{Z_0 tanh(\gamma )- Z_r}{Z_0 tanh(\gamma )+Z_r} \hspace{1in} (23)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
S_{11~oc}= \frac{Z_0 - Z_r tanh(\gamma )}{Z_0 +Z_r tanh(\gamma )} \hspace{1in} (24)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
S_{11~r}= \frac{tanh(\gamma)(Z_0 ^2-Z_r ^2)}{2Z_0Z_r+tanh(\gamma)(Z_0 ^2+Z_r ^2)} \hspace{1in} (25)\nonumber
\end{eqnarray}
%ENDLATEX%
Figure 3
In order to perform the measurements we attached SMA female (flange mount) connectors to each side of the transformer as shown in Figure 3. There are other ways to take into account the effect of the transformer on the measurement, but the easiest way we know so far is just to calibrate the VNA (open, short, load using calibration standards) with the transformer attached to it. In this way (we hope that) the phase and attenuation introduced by the transformer is compensated with the calibration. The setup for the response calibration using the standard load of the VNA () is shown in Figure 4.
Figure 4
After the calibration we attach one end of one of the lines of the stripline directly to the transformer and measure for different loads. Figure 5 shows the setup for the measurement of (line terminated in open circuit). For the end attached to the transformer, we solder one of the wires to the SMA connector body and solder a little pin to the other wire so we can insert it into the SMA receptacle without soldering (you can be more creative). For the measurement of we solder the two wires at the end of the line. For the measurement of 
we solder a resistor to the end of the line.
Figure 5
The figures that come next are all for the line 1 of the McG-SL-w03_007 stripline. A very simple MATLAB code used for calculations and plotting can be found here. Figure 6 shows measured for the line terminated with open circuit and short circuit
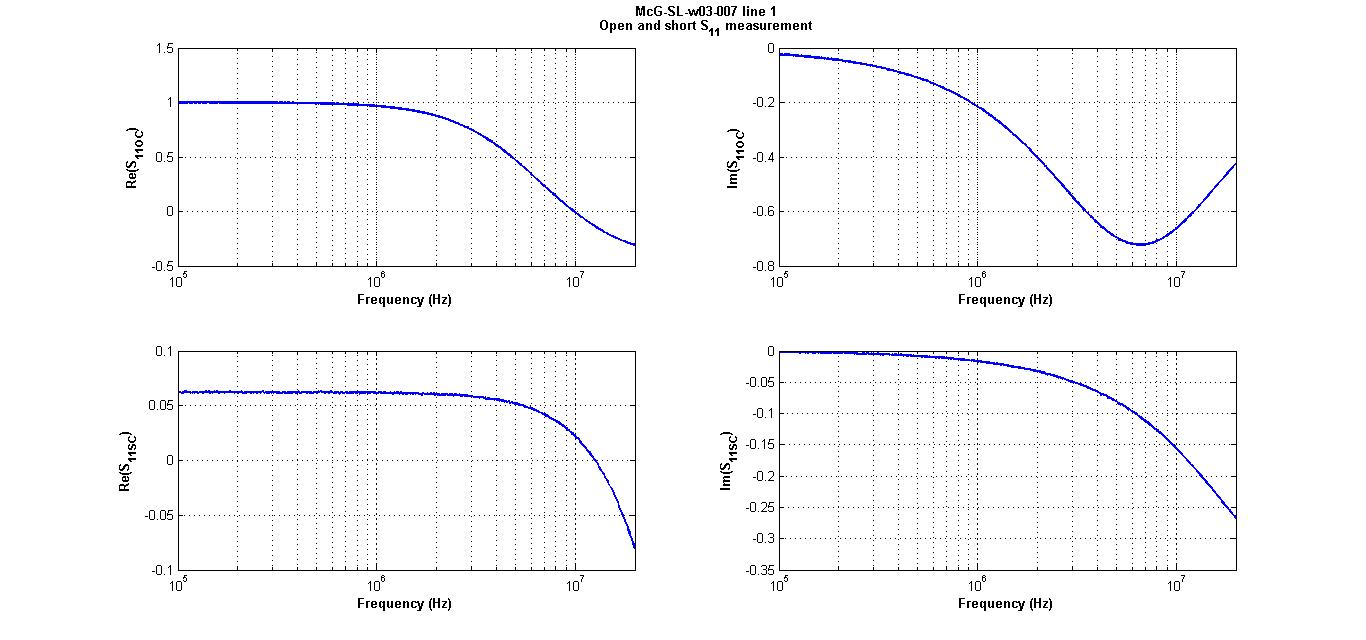Figure 6
Figure 7 shows the characteristic impedance and propagation constant of the line calculated from and
Figure 7
Figure 8 shows the RLGC parameters of the line obtained from and
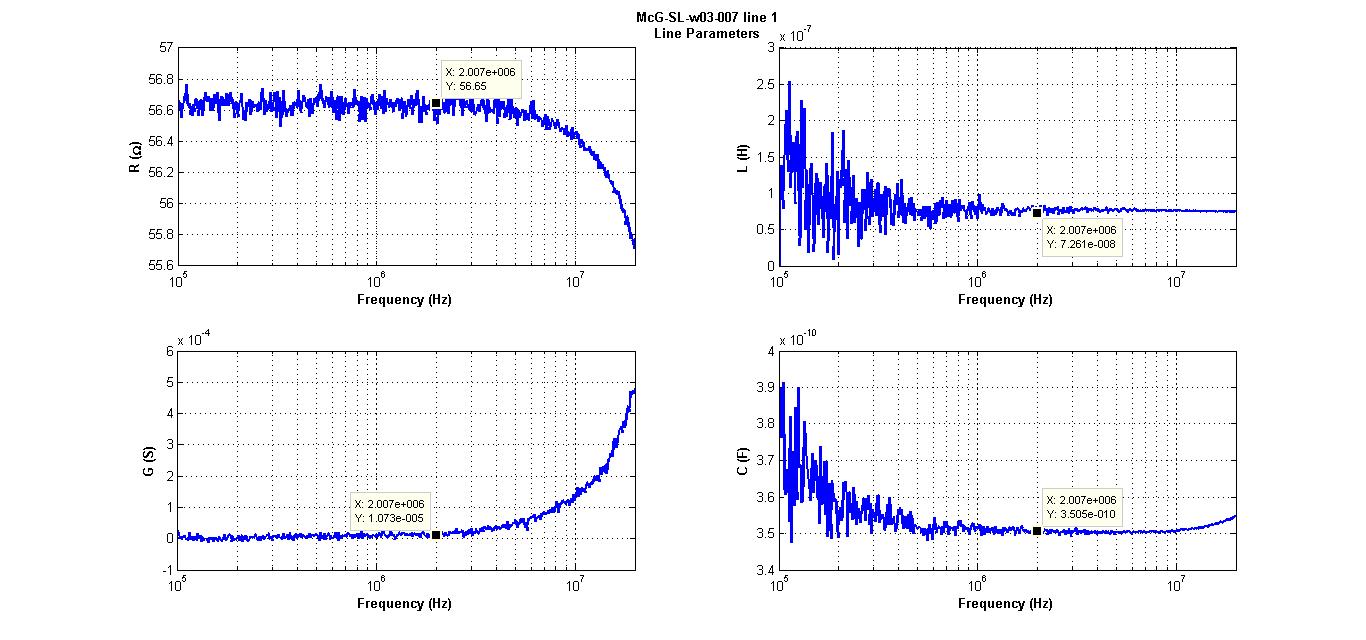Figure 8
So far everything is more or less fine: it seems that we found the RLGC parameters of the line as a function of frequency. From Figure 8 we have that 
and 
at 2 MHz. The resistance is 
. Recall that this is a 27.5'' line. Now some comments.
* I do not know why the values of L and C are so noisy at low frequencies.
* If we consider the line as a parallel plate transmission line then L and C can be determined from and where is the length of the line, is the wire width and is the thickness of the Kapton film, its permittivity and its permeability. With 
, 
, and 
obtain 
and 
. It is clear that this assumption does not apply in this case.
* A parameter of interest for the line is 
. This would be the characteristic impedance of the line at 4 K and is shown in Figure 9. We have 
at 2 MHz.
Figure 9
* Notice that the values of G are very small. Even if it did not happen in this case, below we will see that in some cases we will obtain negatives values of G, and that is unacceptable. It seems that this is not associated to the noise as in case for L and C. The only reason that occurs to me for this to happen is that G is so small that some weird stuff happens when the parameters are calculated. Since I do not know how to explain or fix this, then for now we will ignore the value of G (
). Of course, we have to check that our model with this correction is still able to predict real data. We show this on Figures 10-12 below where we plot the measured for open-circuit, short-circuit and 
loads and compare to the values predicted by our model. Even with we expect that the model works well for the open-circuit and short-circuit case since the parameters were obtained from this data. However, notice that the model also works pretty well for the load case.
Figure 10
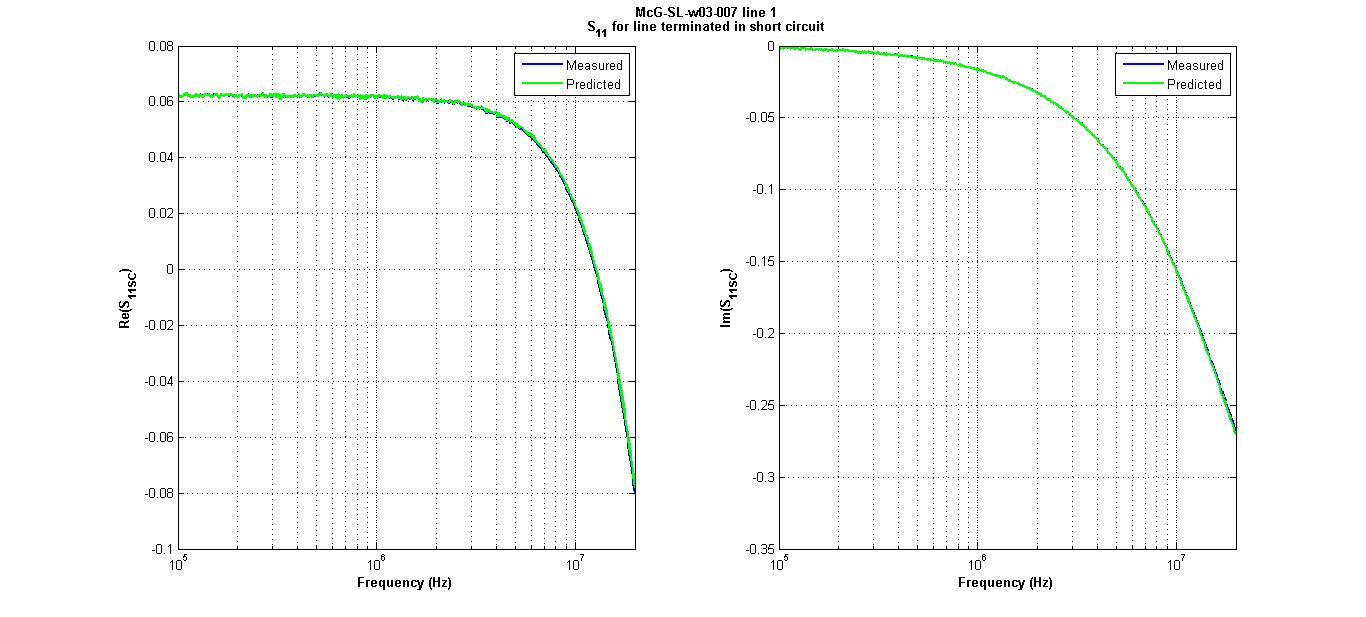Figure 11
Figure 12
Now we apply the same procedure to line 8 of the McG-SL-w03_007 stripline. Figure 13 shows measured for the line terminated with open circuit and short circuit
Figure 13
Figure 14 shows the RLGC parameters of the line. In this case have 
and 
at 2 MHz. and 
at 2 MHz.
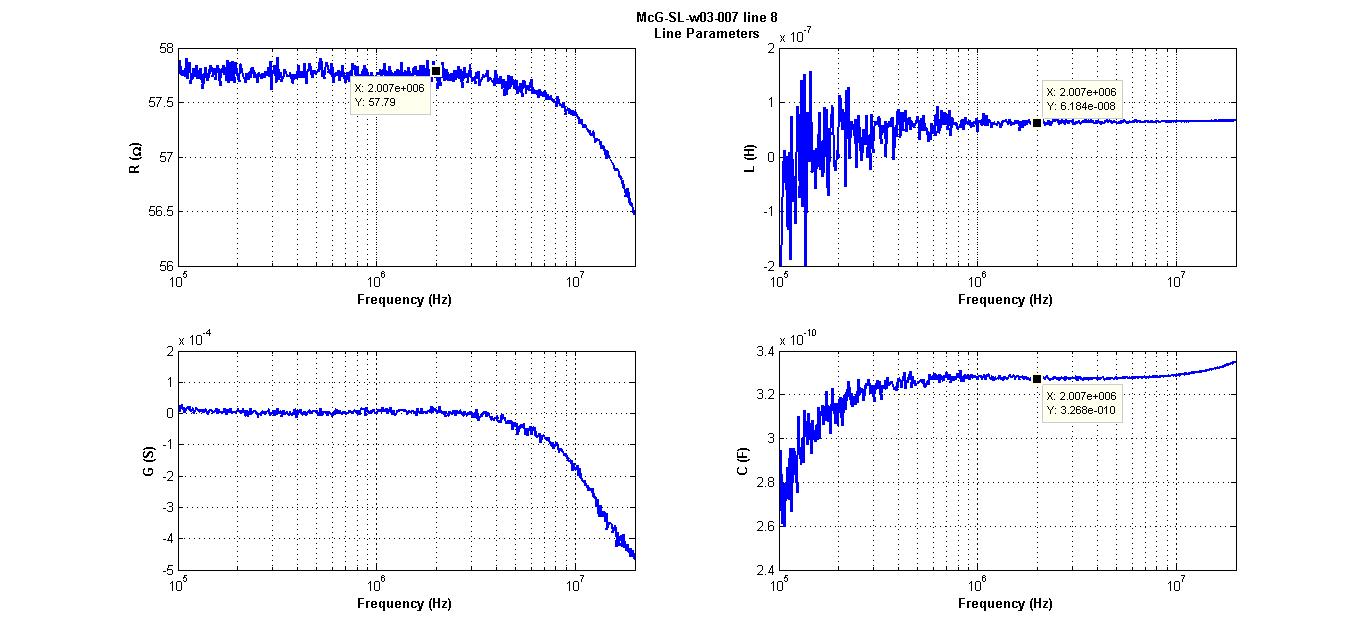Figure 14
As mentioned before, here we see the problem of G taking negative values. We have to investigate a little bit more on why this happens but for now we will take and check that our model works well with this assumption. Even if L seems to take negative values at low frequencies, this seems to be due to the noise that we still cannot explain either (we still have a lot of work!) and its value seems to stabilize after about 500 KHz.
Figure 15 shows a comparison between the model and the measured value of for the line terminated with a load. The model still works well after about 500 KHz. where the value of L seems to stabilize.
Figure 15
We confirmed that the model works well and the values of the RLC parameters of the two lines seem to be consistent (whatever that means). We still have to make more measurements on other striplines to see if we obtain similar values. We also have to make measurements on the 37.5'' striplines to check if the RLC parameters increase linearly with the length of the stripline. In addition, it may be interesting to check if the model still works at high frequencies. I think that it is possible that the model fails in this case because it relies on measurements of open and short-circuits.
This topic: AnalogFMux > WebHome > StriplineCharacterization Topic revision: r14 - 2016-03-02 - WinterlandUser
Superconducting Stripline Characterization
Introduction
This page shows how to characterize the McGill superconducting striplines, that is, how to find the series resistance R, inductance L, conductance G across the stripline, and capacitance C (all per unit length) using the scattering parameters. First we will have to introduce some transmission line theory and find some ugly equations. Then we will apply this theory to the superconducting striplines and find their RLGC parameters using a Vector Network Analyzer.
McGill superconducting striplines
A typical superconducting stripline and the convention for the enumeration of lines (traces) is shown in Figure 1. Each stripline consists of eight NBTi pairs. A single NbTi wire is approximately 29 mil wide and 1 mil thick and the two wires of each pair are separated by 1/3 mil thick Kapton film. Kapton tape of thickness and adhesive is used to pick up the eight lines. The spacing between (borders of) adjacent lines is (ideally) uniform along the stripline and approximately 37.5 mil (66.5 mil between centers). So far, striplines with two different lengths have been produced: 27.5'' and 37.5''. In this wiki we will characterize the lines 1 and 8 of the McG-SL-w03_007 stripline, which is 27.5'' long (including copper ends).
Figure 1
In order to characterize the stripline we will treat each line as a transmission line, that is, we will assume a distributed element model in which the parameters of the line (RLGC) are distributed continuously throughout its material. Now, in practice, the striplines will be used at very low temperatures (about 250mK to 4 K), and in that case the resistance of the NbTi wires is (almost) zero. In general, it is safe to assume for a transmission line that the losses due to the dielectric material (Kapton film in this case) are low so the conductance is also (almost) zero. This means that when used at low temperatures the lines behave as lossless transmission lines and they are completely characterized by their inductance L and capacitance C . Determine L and C for a lossless transmission line is relatively easy. However, in practice it will be very hard to perform measurements on the stripline while keeping it at low temperature, do to the challenges of having to inject and recover the signals through feedthroughs and other wiring. So we choose to characterize the striplines at room temperature.
If you have seen a stripline you may ask why we do not just assume that each line behaves as a parallel plate transmission line in which case, as first approximation, L and C can be determined from and where is the length of the line, is the wire width and is the thickness of the Kapton film, its permittivity and its permeability. Well, the reason is that these equations not only fail in this case, but they fail miserably, as we will see.
This basically means that we will have to measure L and C at room temperature. However we have the additional problem that at room temperature the lines behave as a VERY lossy transmission line because the resistance R of the NbTi wire is about (measured with multimeter). So we will treat each line as a general lossy transmission line. Notice that with this approach we are assuming that the values of L and C that we measure at room temperature will not change (much) as the temperature is decreased to 4 K. However, this assumption is not that crazy: even if we assume a distributed element model for each line without a particular geometry, it makes sense to assume that the parameters of the line depend on its geometry (whatever it is) and maybe on the input so in that case we can expect that these parameters will remain approximately constant as the temperature is decreased (REALLY??).
Some (lossy) transmission line theory
For this section we will assume some familiarity with transmission line theory and S-parameters so we can introduce some concepts without explanation (like the telegrapher's equations, characteristic impedance, propagation constant, etc.) Maybe later we can add a little intro for transmission lines and S-parameters.
Figure 2
For a transmission line like the one shown in Figure 2 above with length , characteristic impedance , load impedance , generator impedance the general Telegrapher's equations can be written as
%BEGINLATEX%
\begin{eqnarray}
\frac{\partial ^2 V(z)}{\partial z^2} &= \gamma ^2 V(z) \hspace{1in} (1) \nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
\frac{\partial ^2 I(z)}{\partial z^2} &= \gamma ^2 I(z) \hspace{1in} (2) \nonumber
\end{eqnarray}
%ENDLATEX%
The solutions for and in the frequency domain are
%BEGINLATEX%
\begin{eqnarray}
V(z)= V^+ e^{-\gamma z}+ V^- e^{\gamma z} \hspace{1in} (3)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
I(z)= \frac{1}{Z_0} \left(V^+ e^{-\gamma z}- V^- e^{\gamma z}\right) \hspace{1in} (4)\nonumber
\end{eqnarray}
%ENDLATEX%
where
%BEGINLATEX%
\begin{eqnarray}
\gamma= \sqrt{(R+j \omega L)(G+j \omega C)} \hspace{1in} (5)\nonumber
\end{eqnarray}
%ENDLATEX%
is the propagation constant and
%BEGINLATEX%
\begin{eqnarray}
Z_0= \sqrt{\frac{R+j \omega L}{G+j \omega C}} \hspace{1in} (6)\nonumber
\end{eqnarray}
%ENDLATEX%
is the characteristic impedance. The constants , are determined by the boundary conditions and are associated with waves traveling in the +z and -z directions respectively. Now, The impedance of the transmission line at a distance z from the load, that is, the load impedance "seen" by a generator placed a distance z from the load is
%BEGINLATEX%
\begin{eqnarray}
Z(z)= \frac{V(z)}{I(z)}=Z_0 \frac{V^+ e^{-\gamma z}+ V^- e^{\gamma z}}{V^+ e^{-\gamma z}- V^- e^{\gamma z}}=Z_0 \frac{1+\Gamma (z)}{1- \Gamma (z)} \hspace{1in} (7) \nonumber
\end{eqnarray}
%ENDLATEX%
where
%BEGINLATEX%
\begin{eqnarray}
\Gamma (z)= \frac{V^-}{V^+} e^{2\gamma z} \hspace{1in} (8)\nonumber
\end{eqnarray}
%ENDLATEX%
is the reflection coefficient, the ratio between in the reflected and incident wave at any point of the transmission line. It is clear from equation (7) that
%BEGINLATEX%
\begin{eqnarray}
\Gamma (z)= \frac{Z(z)-Z_0}{Z(z)+Z_0} \hspace{1in} (9)\nonumber
\end{eqnarray}
%ENDLATEX%
In particular, at the load (z=0)
%BEGINLATEX%
\begin{eqnarray}
\Gamma _L=\frac{V^-}{V^+}= \frac{Z_L-Z_0}{Z_L+Z_0} \hspace{1in} (10)\nonumber
\end{eqnarray}
%ENDLATEX%
So now we can write as
%BEGINLATEX%
\begin{eqnarray}
Z(z)=Z_0 \frac{e^{-\gamma z}+ \frac{\displaystyle Z_L-Z_0}{\displaystyle Z_L+Z_0} e^{\gamma z}}{e^{-\gamma z}- \frac{\displaystyle Z_L-Z_0}{\displaystyle Z_L+Z_0} e^{\gamma z}}=Z_0 \frac{ Z_L \left( e^{\gamma z}+e^{\gamma z} \right)- Z_0 \left( e^{\gamma z}-e^{\gamma z} \right)}{Z_0 \left( e^{\gamma z}+e^{\gamma z} \right)- Z_L \left( e^{\gamma z}-e^{\gamma z} \right)}=Z_0 \frac{Z_L - Z_0 tanh(\gamma z)}{Z_0 - Z_L tanh(\gamma z)} \hspace{1in} (11)\nonumber
\end{eqnarray}
%ENDLATEX%
In particular, the input impedance of the transmission line is
%BEGINLATEX%
\begin{eqnarray}
Z_{in}=Z(-l)=Z_0 \frac{Z_L + Z_0 tanh(\gamma l)}{Z_0 + Z_L tanh(\gamma l)} \hspace{1in} (12)\nonumber
\end{eqnarray}
%ENDLATEX%
Recall that and are complex in general so this equation can be very ugly. There are two special cases: When the load is a short circuit we have
%BEGINLATEX%
\begin{eqnarray}
Z_{in~sc}=Z_0 tanh(\gamma l) \hspace{1in} (13)\nonumber
\end{eqnarray}
%ENDLATEX%
and when the load is an open circuit have
%BEGINLATEX%
\begin{eqnarray}
Z_{in~oc}=\frac{Z_0}{tanh(\gamma l)} \hspace{1in} (14)\nonumber
\end{eqnarray}
%ENDLATEX%
and we have arrived to two very important equations for us
%BEGINLATEX%
\begin{eqnarray}
Z_0=\pm \sqrt{Z_{in~sc}~ Z_{in~oc}} \hspace{1in} (15) \nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
\gamma l=\pm tanh^{-1} \left(\sqrt{\frac{Z_{in~sc}}{Z_{in~oc}}}\right) \hspace{1in} (16)\nonumber
\end{eqnarray}
%ENDLATEX%
We included the sign just to remind you that you will obtain two roots, however only one of them will give you a physically acceptable value. For example, the real part of the propagation constant corresponds to the attenuation constant and its value cannot be negative (I mean, it can be negative but it would have to be interpreted as the attenuation constant for propagation in -z direction). Similarly, the real part of the characteristic impedance, cannot be negative (IS THIS TRUE??.)
Once and are found, the RLGC parameters are determined immediately from equations (5) and (6)
%BEGINLATEX%
\begin{eqnarray}
R=\Re (\gamma Z_0) \hspace{1in} (17)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
L=\frac{\Im (\gamma Z_0)}{\omega} \hspace{1in} (18)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
G=\Re \left( \gamma/Z_0 \right) \hspace{1in} (19)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
C=\frac{\Im (\gamma/Z_0)}{\omega} \hspace{1in} (20)\nonumber
\end{eqnarray}
%ENDLATEX%
where we take meaning that the RLGC parameters are calculated per unit length of the transmission line. Now, for this wiki the only things you need to know about Scattering parameters is that the reflection coefficient is a measurable parameter and that the parameter is just the reflection coefficient at the input of the transmission line. That means that if you connect a transmission line with input impedance to a Vector Network Analyzer (here we will use the Agilent E5071C) with reference impedance (which is generally ) and measure then
%BEGINLATEX%
\begin{eqnarray}
S_{11}= \frac{Z_{in}-Z_r}{Z_{in}+Z_r} \hspace{1in} (21)\nonumber
\end{eqnarray}
%ENDLATEX%
or
%BEGINLATEX%
\begin{eqnarray}
Z_{in}= Z_r \frac{1+S_{11}}{1- S_{11}} \hspace{1in} (22) \nonumber
\end{eqnarray}
%ENDLATEX%
Then, in theory, we have solved the problem of characterizing the transmission line. We can measure with with the transmission line terminated in a short-circuit (call this value ) and find from equation (22). With the same procedure but this time with the transmission line terminated in an open-circuit we can measure and find . Then we can determine and from equations (15) and (16) and finally we can determine the RLGC parameters from equations (17)-(20).
Once the RLGC parameters are determined we can check if our method really works by predicting the value of for an arbitrary load and then comparing with the measured value. In our case we will test our model by measuring with the transmission line terminated with a load . This means that we will have to find expressions for with arbitrary loads. If we substitute from equation (12) into equation (21) obtain
%BEGINLATEX%
\begin{eqnarray}
S_{11}= \frac{Z_0(Z_L-Z_r)+tanh(\gamma)(Z_0 ^2-Z_L Z_r)}{Z_0(Z_L+Z_r)+tanh(\gamma)(Z_0 ^2+Z_L Z_r)} \hspace{1in} (22)\nonumber
\end{eqnarray}
%ENDLATEX%
In the special cases when the load is a short-circuit, open-circuit and () we obtain
%BEGINLATEX%
\begin{eqnarray}
S_{11~sc}= \frac{Z_0 tanh(\gamma )- Z_r}{Z_0 tanh(\gamma )+Z_r} \hspace{1in} (23)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
S_{11~oc}= \frac{Z_0 - Z_r tanh(\gamma )}{Z_0 +Z_r tanh(\gamma )} \hspace{1in} (24)\nonumber
\end{eqnarray}
%ENDLATEX%
%BEGINLATEX%
\begin{eqnarray}
S_{11~r}= \frac{tanh(\gamma)(Z_0 ^2-Z_r ^2)}{2Z_0Z_r+tanh(\gamma)(Z_0 ^2+Z_r ^2)} \hspace{1in} (25)\nonumber
\end{eqnarray}
%ENDLATEX%
Measurements on the McG-SL-w03_007 stripline
Now we will characterize lines 1 and 8 of the McG-SL-w03_007 stripline as an example. In practice, the striplines are used at a frequency of about 2 MHz (I AM NOT REALLY SURE ABOUT THIS) so we will find the RLGC parameters in the range 0.1-20 MHz. As mentioned before we will use the E5071C 100KHz-8.5GHz Network Analyzer for the measurements. Something you have to take into account is that the lines of the striplines are balanced transmission lines while the VNA is an unbalanced system so a balun or transformer must be placed between the VNA and the transmission line. In our case we used the Coilcraft WB2010 transformer. This is a wideband RF transformer with flat frequency response in the range 0.005-100 MHz and 1:1 impedance ratio, so ideally it just transfers or "refers" the input impedance of the transmission line to the unbalanced side without changing it. The datasheet for the WB2010 transformer can be found here.
Figure 3
In order to perform the measurements we attached SMA female (flange mount) connectors to each side of the transformer as shown in Figure 3. There are other ways to take into account the effect of the transformer on the measurement, but the easiest way we know so far is just to calibrate the VNA (open, short, load using calibration standards) with the transformer attached to it. In this way (we hope that) the phase and attenuation introduced by the transformer is compensated with the calibration. The setup for the response calibration using the standard load of the VNA () is shown in Figure 4.
Figure 4
After the calibration we attach one end of one of the lines of the stripline directly to the transformer and measure for different loads. Figure 5 shows the setup for the measurement of (line terminated in open circuit). For the end attached to the transformer, we solder one of the wires to the SMA connector body and solder a little pin to the other wire so we can insert it into the SMA receptacle without soldering (you can be more creative). For the measurement of we solder the two wires at the end of the line. For the measurement of we solder a resistor to the end of the line.
Figure 5
The figures that come next are all for the line 1 of the McG-SL-w03_007 stripline. A very simple MATLAB code used for calculations and plotting can be found here. Figure 6 shows measured for the line terminated with open circuit and short circuit
Figure 6
Figure 7 shows the characteristic impedance and propagation constant of the line calculated from and
Figure 7
Figure 8 shows the RLGC parameters of the line obtained from and
Figure 8
So far everything is more or less fine: it seems that we found the RLGC parameters of the line as a function of frequency. From Figure 8 we have that and at 2 MHz. The resistance is . Recall that this is a 27.5'' line. Now some comments.
* I do not know why the values of L and C are so noisy at low frequencies.
* If we consider the line as a parallel plate transmission line then L and C can be determined from and where is the length of the line, is the wire width and is the thickness of the Kapton film, its permittivity and its permeability. With , , and obtain and . It is clear that this assumption does not apply in this case.
* A parameter of interest for the line is . This would be the characteristic impedance of the line at 4 K and is shown in Figure 9. We have at 2 MHz.
Figure 9
* Notice that the values of G are very small. Even if it did not happen in this case, below we will see that in some cases we will obtain negatives values of G, and that is unacceptable. It seems that this is not associated to the noise as in case for L and C. The only reason that occurs to me for this to happen is that G is so small that some weird stuff happens when the parameters are calculated. Since I do not know how to explain or fix this, then for now we will ignore the value of G (). Of course, we have to check that our model with this correction is still able to predict real data. We show this on Figures 10-12 below where we plot the measured for open-circuit, short-circuit and loads and compare to the values predicted by our model. Even with we expect that the model works well for the open-circuit and short-circuit case since the parameters were obtained from this data. However, notice that the model also works pretty well for the load case.
Figure 10
Figure 11
Figure 12
Now we apply the same procedure to line 8 of the McG-SL-w03_007 stripline. Figure 13 shows measured for the line terminated with open circuit and short circuit
Figure 13
Figure 14 shows the RLGC parameters of the line. In this case have and at 2 MHz. and at 2 MHz.
Figure 14
As mentioned before, here we see the problem of G taking negative values. We have to investigate a little bit more on why this happens but for now we will take and check that our model works well with this assumption. Even if L seems to take negative values at low frequencies, this seems to be due to the noise that we still cannot explain either (we still have a lot of work!) and its value seems to stabilize after about 500 KHz.
Figure 15 shows a comparison between the model and the measured value of for the line terminated with a load. The model still works well after about 500 KHz. where the value of L seems to stabilize.
Figure 15
We confirmed that the model works well and the values of the RLC parameters of the two lines seem to be consistent (whatever that means). We still have to make more measurements on other striplines to see if we obtain similar values. We also have to make measurements on the 37.5'' striplines to check if the RLC parameters increase linearly with the length of the stripline. In addition, it may be interesting to check if the model still works at high frequencies. I think that it is possible that the model fails in this case because it relies on measurements of open and short-circuits.
Conclusion
We showed a method to characterize the McGill superconducting striplines using VNA and assuming a distributed parameter model. We confirmed that the method is accurate in the range 0.1-20 MHz so and we are able to determine the line's inductance and capacitance at room temperature in this range. However, there are still some questions and (little) problems that must be solved, specially the fact that in some cases we obtain negative values of conductance G.
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
 JPG |
8175C_load_cal.JPG | manage | 113.2 K | 2012-04-30 - 20:29 | WinterlandUser | 8175C_load_cal |
| JPG |
S11oc_meas.JPG | manage | 584.4 K | 2012-04-30 - 21:33 | WinterlandUser | S11oc_meas |
 jpg |
SL7_line1_RLGC.jpg | manage | 143.6 K | 2012-05-01 - 13:37 | WinterlandUser | SL7_line1_RLGC_new |
| jpg |
SL7_line1_RLGC_new.jpg | manage | 143.6 K | 2012-05-01 - 13:38 | WinterlandUser | SL7_line1_RLGC_new |
| jpg |
SL7_line1_S11oc_model.jpg | manage | 120.0 K | 2012-05-01 - 14:02 | WinterlandUser | SL7_line1_S11oc_model |
| jpg |
SL7_line1_S11r_model.jpg | manage | 120.3 K | 2012-05-01 - 14:03 | WinterlandUser | SL7_line1_S11r_model |
| jpg |
SL7_line1_S11sc_S11oc.jpg | manage | 121.9 K | 2012-05-01 - 00:37 | WinterlandUser | SL7_line1_S11sc_S11oc |
| jpg |
SL7_line1_S11sc_model.jpg | manage | 120.4 K | 2012-05-01 - 14:02 | WinterlandUser | SL7_line1_S11sc_model |
| jpg |
SL7_line1_Z0_gamma.jpg | manage | 132.3 K | 2012-05-01 - 00:51 | WinterlandUser | SL7_line1_Z0_gamma |
| jpg |
SL7_line1_sqrtLoverC.jpg | manage | 97.4 K | 2012-05-01 - 02:24 | WinterlandUser | SL7_line1_sqrtLoverC |
| jpg |
SL7_line8_RLGC.jpg | manage | 131.3 K | 2012-05-01 - 14:24 | WinterlandUser | SL7_line8_RLGC |
| jpg |
SL7_line8_S11r_model.jpg | manage | 122.2 K | 2012-05-01 - 14:42 | WinterlandUser | SL7_line8_S11r_model |
| jpg |
SL7_line8_S11sc_S11oc.jpg | manage | 126.2 K | 2012-05-01 - 14:23 | WinterlandUser | SL7_line8_S11sc_S11oc |
| JPG |
WB2010.JPG | manage | 422.3 K | 2012-04-30 - 19:56 | WinterlandUser | WB2010 |
| m |
osltlextract.m | manage | 9.0 K | 2012-05-01 - 00:43 | WinterlandUser | osltlextract.m |
 pdf |
showpdf.pdf | manage | 112.2 K | 2012-04-30 - 19:45 | WinterlandUser | WB2010_datasheet |
| JPG |
stripline_and_convention.JPG | manage | 108.3 K | 2012-04-30 - 13:30 | WinterlandUser | stripline_and_convention |
| jpg |
stripline_model.jpg | manage | 7.5 K | 2012-06-07 - 02:46 | MattDobbs | |
| jpg |
transmission_line.jpg | manage | 13.7 K | 2012-04-30 - 00:19 | WinterlandUser | transmission_line |
This topic: AnalogFMux > WebHome > StriplineCharacterization Topic revision: r14 - 2016-03-02 - WinterlandUser
© 2020 Winterland Cosmology Lab, McGill University, Montréal, Québec, Canada