---+++ Amplifier Noise gain derivation (General derivation applicable to squids and transformers)
Before looking at our actual circuit diagram, consider the following diagram
* NoiseGainDiagram.jpg:
 The following equations describe the gain between the output voltage and the noise voltage.
The following equations describe the gain between the output voltage and the noise voltage.
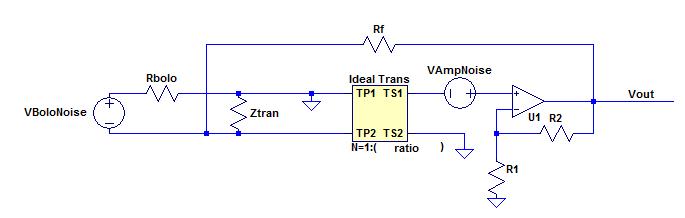 For the purposes of this analysis assume that the bolometer noise voltage = 0V i.e a short.
Firstly defining Zin as the Bolometer resistance in parallel with the Transformer input impedance.
(Ideally the transformer input impedance = inf, but having a magnetizing inductance and a winding capacitance reduces this)
For the purposes of this analysis assume that the bolometer noise voltage = 0V i.e a short.
Firstly defining Zin as the Bolometer resistance in parallel with the Transformer input impedance.
(Ideally the transformer input impedance = inf, but having a magnetizing inductance and a winding capacitance reduces this)
 * AmpNoiseEquivSim.jpg:
* AmpNoiseEquivSim.jpg:
 We can see that when the transformer input impedance is very large (Lp huge and Cp tiny), both the Squid and Transformer based systems look equivalent in terms of the amplifier noise gain.
Note also that we could have predicted the noise gain. For the transformer Rf/(N* (Rbolo//Ztran) ) => 21.9dB at DC and for the Squid based system Rf*Zsquid/(G* (Rbolo//Zsquid)) => 21.9dB at DC. Additionally we could also predict that at 1.06Mhz for the squid based system the gain will be 3dB higher. This is because at 1.06Mhz, the impedance of the Squid inductor = 1 Ohm.
Yay, everything makes sense.
Now making L such that at 25kHz we have 1 Ohm impedance gives L=6.4uH and doing the same for C at 500kHz gives 0.32uF
Simulating the circuit gives:
* AmpNoiseEquivSim2.jpg:
We can see that when the transformer input impedance is very large (Lp huge and Cp tiny), both the Squid and Transformer based systems look equivalent in terms of the amplifier noise gain.
Note also that we could have predicted the noise gain. For the transformer Rf/(N* (Rbolo//Ztran) ) => 21.9dB at DC and for the Squid based system Rf*Zsquid/(G* (Rbolo//Zsquid)) => 21.9dB at DC. Additionally we could also predict that at 1.06Mhz for the squid based system the gain will be 3dB higher. This is because at 1.06Mhz, the impedance of the Squid inductor = 1 Ohm.
Yay, everything makes sense.
Now making L such that at 25kHz we have 1 Ohm impedance gives L=6.4uH and doing the same for C at 500kHz gives 0.32uF
Simulating the circuit gives:
* AmpNoiseEquivSim2.jpg:
 Looking at the appropriate gain curve (the green one) we see that at 25kHz we have a 3dB increase in noise gain and similarly at 500kHz we have the same thing.
So, to summarize, the bandwidth of the transformer noise amplification is defined by Rbolo // Ztran.
* AmplifierNoiseAnalysisSquidTran.cir: Spice netlist for above amplifier noise simulations
Looking at the appropriate gain curve (the green one) we see that at 25kHz we have a 3dB increase in noise gain and similarly at 500kHz we have the same thing.
So, to summarize, the bandwidth of the transformer noise amplification is defined by Rbolo // Ztran.
* AmplifierNoiseAnalysisSquidTran.cir: Spice netlist for above amplifier noise simulations

This topic: ColdFeedback > WebHome > AmplifierNoiseAmplification Topic revision: r5 - 2010-03-03 - WinterlandUser
 The following equations describe the gain between the output voltage and the noise voltage.
The following equations describe the gain between the output voltage and the noise voltage.
Vout=G*VAmplifierInput VAmplifierInput= Vout * (-FeedbackGain)+Vn Vout=G*VAmplifierInput=G * (Vn-Vout*FeedbackGain)Solving for Vout gives:
Vout/Vn= 1 / (1/G + FeedbackGain)For G>>FeedbackGain
Vout/Vn= 1 / FeedbackGain
Amplifier Noise gain derivation (applicable to transformers)
Now looking at our feedback topology : * FeedbackDiagram.jpg: For the purposes of this analysis assume that the bolometer noise voltage = 0V i.e a short.
Firstly defining Zin as the Bolometer resistance in parallel with the Transformer input impedance.
(Ideally the transformer input impedance = inf, but having a magnetizing inductance and a winding capacitance reduces this)
For the purposes of this analysis assume that the bolometer noise voltage = 0V i.e a short.
Firstly defining Zin as the Bolometer resistance in parallel with the Transformer input impedance.
(Ideally the transformer input impedance = inf, but having a magnetizing inductance and a winding capacitance reduces this)
Zin = Rbolo // ZtranA signal at the output of the amplifier is coupled to the input of the transformer via the feedback resistor which is in series with Zin. The voltage across Zin is equal to the voltage across the primary. Note that Rf and Zin form a potential divider.
FeedbackGain=N*Zin /( Zin + Rf) Vout/Vn=( Zin + Rf) / N*Zinfor Zin<<Rf (since Rbolo << Rf)
Vout/Vn = Rf/(N*Zin) ) = Rf/(N* Rbolo//Ztran )So, from the amplifier noise perspective, the frequency response of the noise gain is determined by the bolometer resistance in parallel with the primary referred transformers 'parasitics' If we wish to have 3dB's in the Noise gain at 50kHz and 500kHz, and have an Rbolo of 1 Ohm, at 50kHz => XL=j Rbolo Ohms and at 500kHz XC=-j Rbolo Ohms This places a constraint on Lprimary > Rbolo / (2*pi*fmin) = 1 Ohm / (2 * pi * fmin) = 3.1uH and a constraint on Cprimary < 1/(2*pi*fmax*Rbolo) = 0.32uF If these constraints are met, in the pass band, where Rbolo//Ztran approximates Rbolo
Vout/Vn = Rf/(N*Rbolo) = (V/A) / NRemember that the output voltage due to the bolometer current is :
Vout/In = Rf/(Rbolo) = (V/A)So, if we meet the conditions specified here, the signal to noise in the pass band can be expressed as follows:
S/N = N * In / VnIf we aim for S/N of 1, with 5pA/sqrt(Hz) of bolometer current noise this places a condition on the transformer turns ratio of N = 200 turns / nV of amplifier voltage noise
Amplifier Noise gain derivation (applicable to Squids)
For the squid based system there is a subtle difference in the feedbackgain equation. (Put a diagram in later)Ifeedback = Vout/(Zsquid//Rbolo + Rf) Isquid=Ifeedback * Rbolo/(Rbolo+Zsquid) --current divider FeedbackGain=Gsquid*Isquid/Vout = Gsquid* (1/(Zsquid//Rbolo + Rf)) * Rbolo/(Rbolo+Zsquid)Assuming that Zsquid//Rbolo << Rf
FeedbackGain= Gsquid* (1/Rf) * Rbolo/(Rbolo+Zsquid)Assuming that Zsquid << Rbolo (Trevors assumption)
FeedbackGain= Gsquid* (1/Rf) * Rbolo/(Rbolo) = Gsquid/RfCompare this with FeedbackGain=N*Zin/Rf for the transformer. The Zin factor is what is causing our transformer problems. Having Zin > 1 will fix these problems though. So, for a Squid with 400A/V, an amplifier noise of 1nV/sqrt(Hz), a feedback resistance of 5kOhms and a bolometer resistance of 1 Ohm at 500mK we get (Trevors assumption is certainly valid at low frequency)
Vout noise due to bolometer = 5.3pA/sqrt(Hz) * 5000/1 = 26.3nV/sqrt(Hz) Vout noise due to amplifier = 1nV * Rf/Gsquid = 12.5nV/sqrt(Hz) Vout total noise = 29.2nV/sqrt(Hz)Referring this noise to the bolometer gives: 29.2nV/sqrt(Hz) / 5000 = 5.8pA/sqrt(Hz)
Comparing the Squid and transformer system in simulation
For now just looking at the amplifier noise properties * AmpNoiseEquivCirc.jpg: * AmpNoiseEquivSim.jpg:
* AmpNoiseEquivSim.jpg:  We can see that when the transformer input impedance is very large (Lp huge and Cp tiny), both the Squid and Transformer based systems look equivalent in terms of the amplifier noise gain.
Note also that we could have predicted the noise gain. For the transformer Rf/(N* (Rbolo//Ztran) ) => 21.9dB at DC and for the Squid based system Rf*Zsquid/(G* (Rbolo//Zsquid)) => 21.9dB at DC. Additionally we could also predict that at 1.06Mhz for the squid based system the gain will be 3dB higher. This is because at 1.06Mhz, the impedance of the Squid inductor = 1 Ohm.
Yay, everything makes sense.
Now making L such that at 25kHz we have 1 Ohm impedance gives L=6.4uH and doing the same for C at 500kHz gives 0.32uF
Simulating the circuit gives:
* AmpNoiseEquivSim2.jpg:
We can see that when the transformer input impedance is very large (Lp huge and Cp tiny), both the Squid and Transformer based systems look equivalent in terms of the amplifier noise gain.
Note also that we could have predicted the noise gain. For the transformer Rf/(N* (Rbolo//Ztran) ) => 21.9dB at DC and for the Squid based system Rf*Zsquid/(G* (Rbolo//Zsquid)) => 21.9dB at DC. Additionally we could also predict that at 1.06Mhz for the squid based system the gain will be 3dB higher. This is because at 1.06Mhz, the impedance of the Squid inductor = 1 Ohm.
Yay, everything makes sense.
Now making L such that at 25kHz we have 1 Ohm impedance gives L=6.4uH and doing the same for C at 500kHz gives 0.32uF
Simulating the circuit gives:
* AmpNoiseEquivSim2.jpg:  Looking at the appropriate gain curve (the green one) we see that at 25kHz we have a 3dB increase in noise gain and similarly at 500kHz we have the same thing.
So, to summarize, the bandwidth of the transformer noise amplification is defined by Rbolo // Ztran.
* AmplifierNoiseAnalysisSquidTran.cir: Spice netlist for above amplifier noise simulations
Looking at the appropriate gain curve (the green one) we see that at 25kHz we have a 3dB increase in noise gain and similarly at 500kHz we have the same thing.
So, to summarize, the bandwidth of the transformer noise amplification is defined by Rbolo // Ztran.
* AmplifierNoiseAnalysisSquidTran.cir: Spice netlist for above amplifier noise simulations
Noise gain of bolometer in Transformer based system
If the amplifier noise gain criteria for our system are met. It implies that at the 3dB limits we have XLp or XCp= 1Ohm. This implies that when we place the feedback around the circuit, the input impedance is total defined by Rf/(N*G) (since this is much smaller than 1 Ohm) and will remain constant across the full bandwidth resulting in a constant Vout/Ibolo across the bandwidth of interest.Matt's notes:
High adam and Kevin. Linked below are plots from my own simulations (using your parameters), which essentially agree with your conclusions. I them use the parameters that are roughly the ones from the original suggestion for our system (these are rough choices) and re-plot both the signal and noise, to find that there exists a buildable redesign transformer that fits this parameter space. Do you agree that the results of the noise and transimpedance simulations are realistic and the conclusions valid? Isn't this very close to what we built and have in the cryostat right now? If so, isn't this good? * 2010-03-02_SquidLessTransfAddressAdamsCalcs.pdf: writeupExplanation for simulation differences:
MacSpice seems to be only plotting the real part of what its being asked to plot. Its unfortunately not giving the amplitude. Perhaps we can get it to plot the correct solution by changing the plot formula to sqrt(Re(V(nampout))^2+Im(V(nampout))^2) * realimagnoisecomponents2.jpg:
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
2010-03-02_SquidLessTransfAddressAdamsCalcs.pdf | manage | 127.7 K | 2010-03-02 - 20:42 | MattDobbs | writeup |
| |
AmpNoiseEquivCirc.jpg | manage | 51.7 K | 2010-03-01 - 21:17 | WinterlandUser | |
| |
AmpNoiseEquivSim.jpg | manage | 77.4 K | 2010-03-01 - 21:19 | WinterlandUser | |
| |
AmpNoiseEquivSim2.jpg | manage | 87.7 K | 2010-03-01 - 21:35 | WinterlandUser | |
| |
AmplifierNoiseAnalysisSquidTran.cir | manage | 0.9 K | 2010-03-01 - 21:48 | WinterlandUser | Spice netlist for above amplifier noise simulations |
| |
FeedbackDiagram.jpg | manage | 15.2 K | 2010-03-01 - 16:24 | WinterlandUser | |
| |
NoiseGainDiagram.jpg | manage | 9.0 K | 2010-03-01 - 16:32 | WinterlandUser | |
| |
realimagnoisecomponents.jpg | manage | 149.3 K | 2010-03-03 - 22:06 | WinterlandUser | |
| |
realimagnoisecomponents2.jpg | manage | 71.0 K | 2010-03-03 - 22:11 | WinterlandUser |
This topic: ColdFeedback > WebHome > AmplifierNoiseAmplification Topic revision: r5 - 2010-03-03 - WinterlandUser
© 2020 Winterland Cosmology Lab, McGill University, Montréal, Québec, Canada

