---+ Transformers in the cryostat
Two transformers present
On SQ1:
300:1
16 Ohm secondary (A38-B38) SQout
0.6 Ohm primary (A40-B40)
On SQ8:
200:1 70nH/turn^2
10mH 6.3Ohm secondary (A3-B3) SQout
0.4Ohm primary (A5-B5)
 From the figure the flat noise level of the OPA847 circuit is 1.8uV/sqrt(Hz) and similarly for the ADA4817 there is 5.1uV/sqrt(Hz)
Note that repeating the measurements results in similar figures i.e the spikes in the noise response of the OPA847 are indeed there (690kHz and 6.1Mhz)
* 200x averaged 10kHz resolution bandwidth
NoiseFloor10OhmRB10k.mat: Raw data for 10k Resolution bandwidth figure
From the figure the flat noise level of the OPA847 circuit is 1.8uV/sqrt(Hz) and similarly for the ADA4817 there is 5.1uV/sqrt(Hz)
Note that repeating the measurements results in similar figures i.e the spikes in the noise response of the OPA847 are indeed there (690kHz and 6.1Mhz)
* 200x averaged 10kHz resolution bandwidth
NoiseFloor10OhmRB10k.mat: Raw data for 10k Resolution bandwidth figure
 With a larger resolution bandwidth the spikes in the spectrum can no longer be seen - note also that the low frequency part of the response is more flat
With a larger resolution bandwidth the spikes in the spectrum can no longer be seen - note also that the low frequency part of the response is more flat
 The spikes are now visible on this OpAmp (250kHz,645kHz,690kHz,1.2Mhz ,1.9kHz, 2.2Mhz, 3.8MHz). The spikes are at different frequencies to the previous OPA847.
The noise level is typically 9.1uV/sqrt(Hz) in the pass band
The spikes are now visible on this OpAmp (250kHz,645kHz,690kHz,1.2Mhz ,1.9kHz, 2.2Mhz, 3.8MHz). The spikes are at different frequencies to the previous OPA847.
The noise level is typically 9.1uV/sqrt(Hz) in the pass band
ADA481gain.mat: Source data for figure I currently do not understand why the gain is 1210 at the peak. I was expecting 826 as stated earlier.
Note also that when looking at the noise plots shown earlier, the input noise to the ADA4817 is 4nV/sqrt(Hz) and the output noise of the amplifier is 5.1uV/sqrt(Hz) giving a gain of 1275
Strange...... Have a feeling that the component values on the Lisa board for Channel 1 is not the same as that on the schematic
* Frequency response overlaid with the 10Ohm noise scaled up by 235x:
I currently do not understand why the gain is 1210 at the peak. I was expecting 826 as stated earlier.
Note also that when looking at the noise plots shown earlier, the input noise to the ADA4817 is 4nV/sqrt(Hz) and the output noise of the amplifier is 5.1uV/sqrt(Hz) giving a gain of 1275
Strange...... Have a feeling that the component values on the Lisa board for Channel 1 is not the same as that on the schematic
* Frequency response overlaid with the 10Ohm noise scaled up by 235x:
 Note that although the 235x was chosen to visually allow the easiest shape comparison, it can be calculated approximately from 1/( 1e6 x OpAmp input noise)
Note that although the 235x was chosen to visually allow the easiest shape comparison, it can be calculated approximately from 1/( 1e6 x OpAmp input noise)

 From the above frequency response data, the gain peaks at +61.7dB giving 1216 V/V with a bandwidth of 350kHz
From the above frequency response data, the gain peaks at +61.7dB giving 1216 V/V with a bandwidth of 350kHz
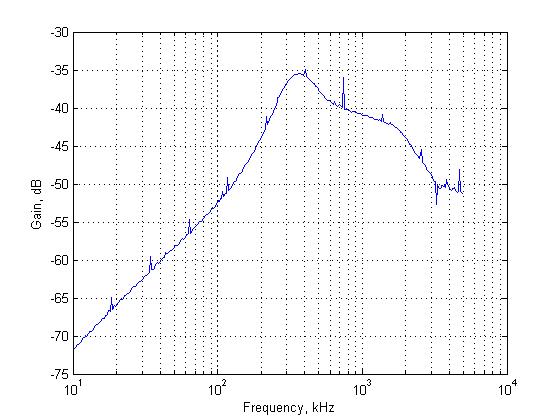
 I would firstly predict that the resonant frequency is at 1/(2*Pi*sqrt(1uH *236pF*30^2)) = 345kHz, secondly I would predict that the gain at resonance (when the input impedance of the transformer is ideally infinite - think parallel LC) is 0.1/(50.1) i.e the voltage gain is independent of the 5.1Ohm resistor = 30*2e-3V/V => -24.4dB
The graph shows -35dB's we are loosing 10.6dB somewhere. This points to the transformer having a large leakage inductance (bad coupling) , for instance 0.71uH leakage and 0.29uH magnetizing. To improve this, much more windings are required on the primary, and if possible the windings should be directly over each other. Alternatively the peak gain is consistent with a load of 2kOhms present on the secondary - thus forming a divider with the 5.1Ohm. Perhaps we have some combination of these two processes taking place.
Just to be sure that the transformer has been characterized properly. Here are results taken by feeding a 10V p-p signal from the function generator into the transformer(with matching circuitry) for both a 10k load and open load on the transformer secondary. An oscilloscope is used to read both the input and output of the network, both channels being on the 1MOhm input impedance setting. Note that we're getting very close to the predicted transformer gain. This points to some additional loading taking place on the Lisa board at the input to the amplifier i.e I believe that we're having some potential divider going on.
* Transformer (and matching circuitry) frequency response taken by hand:
I would firstly predict that the resonant frequency is at 1/(2*Pi*sqrt(1uH *236pF*30^2)) = 345kHz, secondly I would predict that the gain at resonance (when the input impedance of the transformer is ideally infinite - think parallel LC) is 0.1/(50.1) i.e the voltage gain is independent of the 5.1Ohm resistor = 30*2e-3V/V => -24.4dB
The graph shows -35dB's we are loosing 10.6dB somewhere. This points to the transformer having a large leakage inductance (bad coupling) , for instance 0.71uH leakage and 0.29uH magnetizing. To improve this, much more windings are required on the primary, and if possible the windings should be directly over each other. Alternatively the peak gain is consistent with a load of 2kOhms present on the secondary - thus forming a divider with the 5.1Ohm. Perhaps we have some combination of these two processes taking place.
Just to be sure that the transformer has been characterized properly. Here are results taken by feeding a 10V p-p signal from the function generator into the transformer(with matching circuitry) for both a 10k load and open load on the transformer secondary. An oscilloscope is used to read both the input and output of the network, both channels being on the 1MOhm input impedance setting. Note that we're getting very close to the predicted transformer gain. This points to some additional loading taking place on the Lisa board at the input to the amplifier i.e I believe that we're having some potential divider going on.
* Transformer (and matching circuitry) frequency response taken by hand:

 * Chan1Chan8FSweepPhase.jpg:
* Chan1Chan8FSweepPhase.jpg:
 The bandwidth on both channels appears to be approximately 950kHz. This is smaller than the expected 2Mhz, calculated from the 1GHz bandwidth and circuit gain of 500.
Even through the the open loop gain of the amplifier is low, from see p.2 http://users.ece.gatech.edu/mleach/ece3050/notes/OpAmps/opampbw.pdf or the attached file opampbw.pdf the gain bandwidth product should still hold.
Additionally the drop of rate is approximately -20dB/decade which is consistant with a first order amplifier.
The bandwidth on both channels appears to be approximately 950kHz. This is smaller than the expected 2Mhz, calculated from the 1GHz bandwidth and circuit gain of 500.
Even through the the open loop gain of the amplifier is low, from see p.2 http://users.ece.gatech.edu/mleach/ece3050/notes/OpAmps/opampbw.pdf or the attached file opampbw.pdf the gain bandwidth product should still hold.
Additionally the drop of rate is approximately -20dB/decade which is consistant with a first order amplifier.
 *VBolo- is grounded via one of the feedback lines *
*VBolo- is grounded via one of the feedback lines *
 * Chan8 Noise vs R:
* Chan8 Noise vs R:
 The noise measurements in the flat regions of the above figures are consistent with that expected.
For a 0Ohm load, the expected noise is 835 x 4nV/sqrt(Hz) = 3.3uV/sqrt(Hz)
For a 1kOhm load, the expected noise is as follows:
Noise=sqrt(4*Kb*T*R)=0.13*Sqrt(R) nV/sqrt(Hz) = 4.1nV/sqrt(Hz) at 300k. The amplifier noise is 4nV/sqrt(Hz) which adds in quadrature. The total expected noise is therefore 5.7nV*835=4.8uV/sqrt(Hz)
For a 10kOhm load the expected noise is:
13nV/sqrt(Hz) in quadrature with 4nV/sqrt(Hz), multiplied by 835 = 11.4uV/sqrt(Hz)
Note that the noise Spikes seen at 830kHz are not related to the GPIB and we believe them to be radio based
The noise measurements in the flat regions of the above figures are consistent with that expected.
For a 0Ohm load, the expected noise is 835 x 4nV/sqrt(Hz) = 3.3uV/sqrt(Hz)
For a 1kOhm load, the expected noise is as follows:
Noise=sqrt(4*Kb*T*R)=0.13*Sqrt(R) nV/sqrt(Hz) = 4.1nV/sqrt(Hz) at 300k. The amplifier noise is 4nV/sqrt(Hz) which adds in quadrature. The total expected noise is therefore 5.7nV*835=4.8uV/sqrt(Hz)
For a 10kOhm load the expected noise is:
13nV/sqrt(Hz) in quadrature with 4nV/sqrt(Hz), multiplied by 835 = 11.4uV/sqrt(Hz)
Note that the noise Spikes seen at 830kHz are not related to the GPIB and we believe them to be radio based

 The spice simulation data for these two configurations can be seen in the following figure:
The spice simulation data for these two configurations can be seen in the following figure:
 The spectrum analyzer measurements are as follows:
The spectrum analyzer measurements are as follows:
 Interestingly the spice configuration with the 15nH inductance in series with the 0.1Ohm bias resistor provides the most accurate model.
Interestingly the spice configuration with the 15nH inductance in series with the 0.1Ohm bias resistor provides the most accurate model.
 Using the above circuit as a front end to the Squid control board amplifier should result in a peak gain, at a resonant frequency of f=1/(2*Pi*sqrt(1mH*236pF))=328kHz. Note that the 1mH in the calculation is the reflected value of the primary inductance to the secondary. The gain, at that resonant frequency is expected to be 20log( (0.1/50)*30*835 )=+34dB. Note that the 0.1/50 corresponds to the potential divider at the front of the transformer stage and the 30 corresponds to the transformer voltage gain. At resonance the reactive components (since they are in parallel) have 'infinite' impedance and hence disappear from the calculation.
Testing the system frequency response on the Spectrum analyzer results in the following figures.
* Gain vs Frequency for Transformer and Squid control board amplifier:
Using the above circuit as a front end to the Squid control board amplifier should result in a peak gain, at a resonant frequency of f=1/(2*Pi*sqrt(1mH*236pF))=328kHz. Note that the 1mH in the calculation is the reflected value of the primary inductance to the secondary. The gain, at that resonant frequency is expected to be 20log( (0.1/50)*30*835 )=+34dB. Note that the 0.1/50 corresponds to the potential divider at the front of the transformer stage and the 30 corresponds to the transformer voltage gain. At resonance the reactive components (since they are in parallel) have 'infinite' impedance and hence disappear from the calculation.
Testing the system frequency response on the Spectrum analyzer results in the following figures.
* Gain vs Frequency for Transformer and Squid control board amplifier:
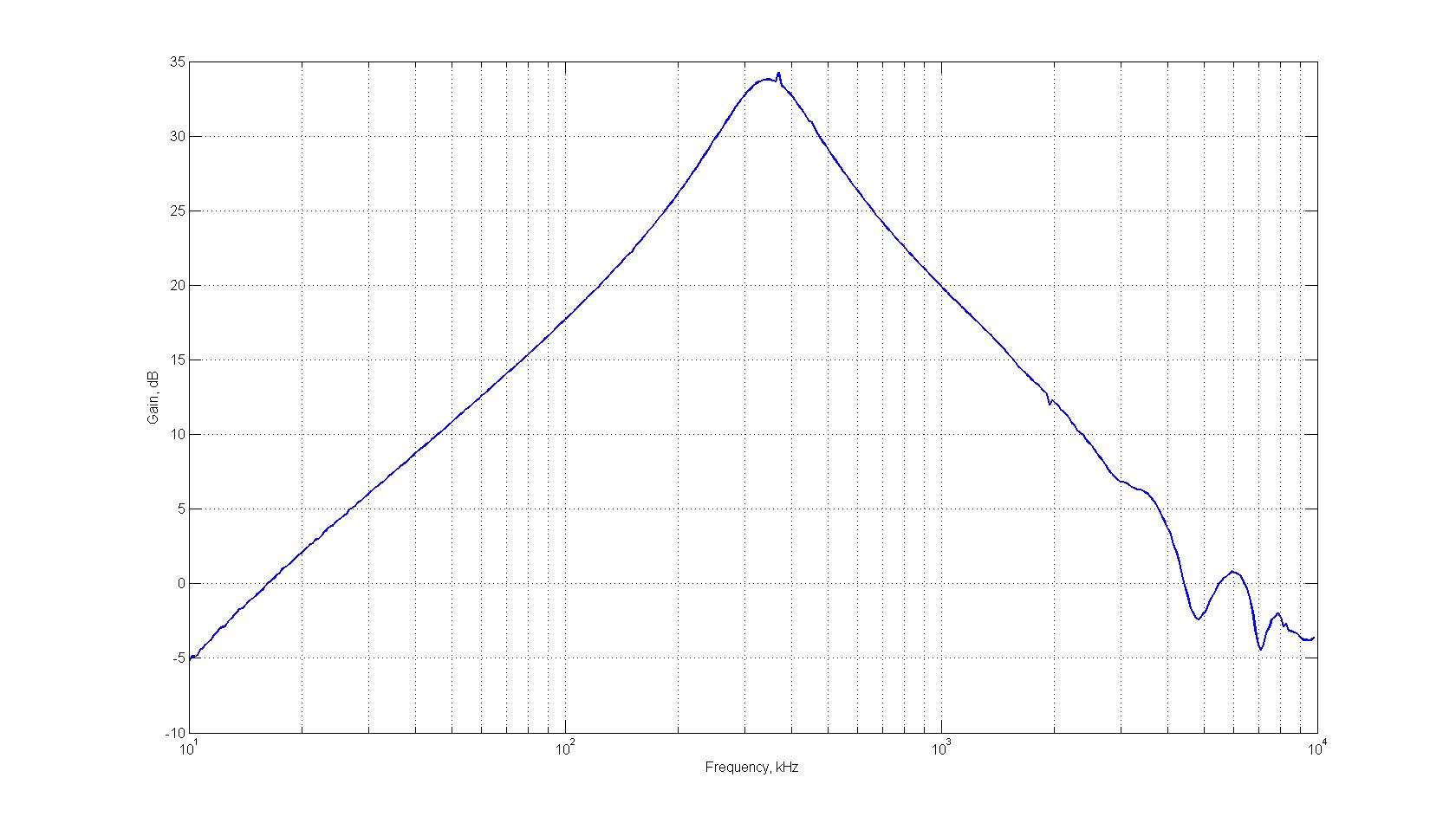 * Phase vs Frequency for Transformer and Squid control board amplifier:
* Phase vs Frequency for Transformer and Squid control board amplifier:
 It can be seen from the measured frequency response that the peak gain and associated frequency are as expected.
It can be seen from the measured frequency response that the peak gain and associated frequency are as expected.
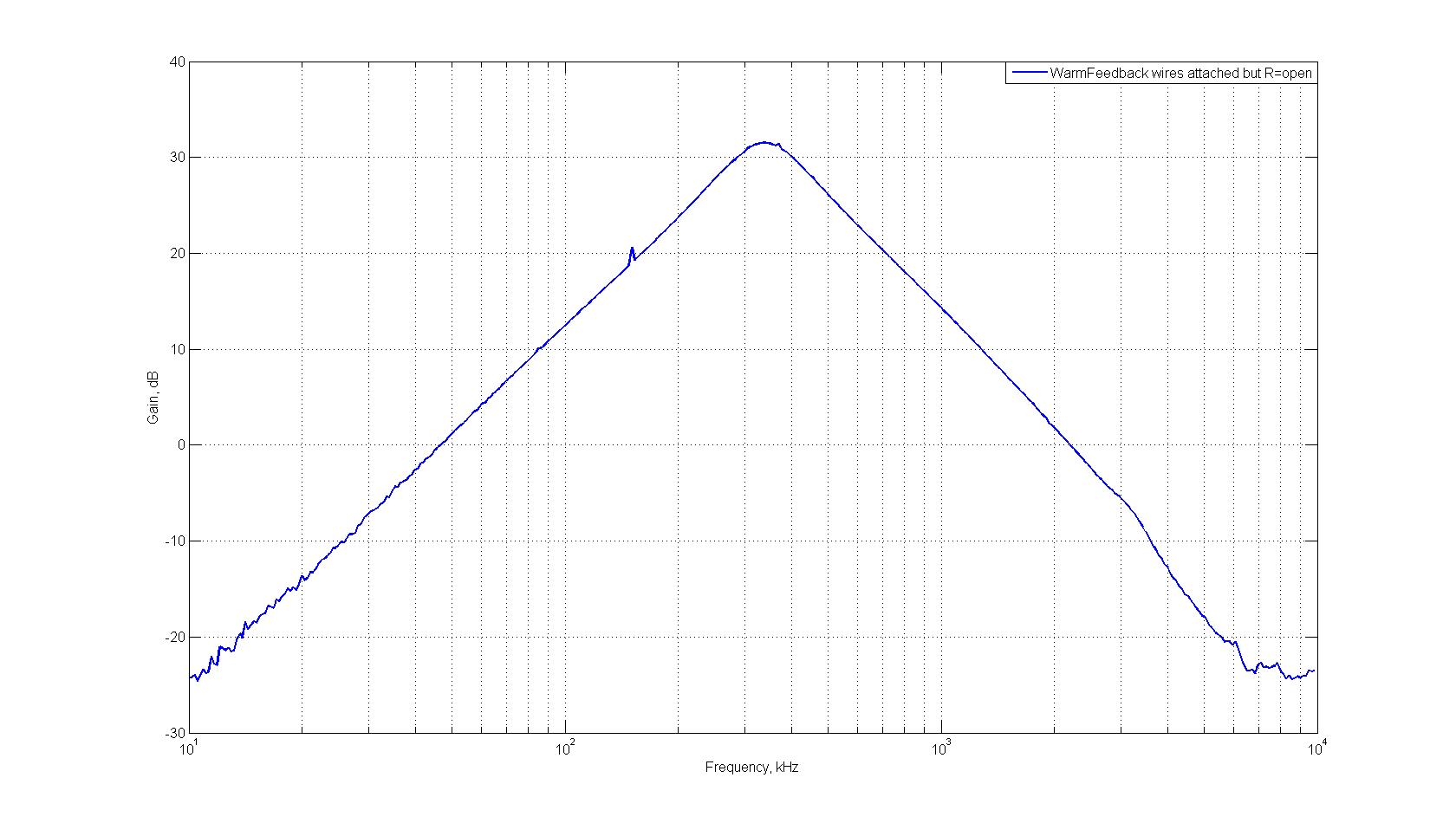 * WarmFeedbackPhaseOpen.jpg:
* WarmFeedbackPhaseOpen.jpg:
 We can see that there appears to be a 2dB reduction in peak gain when plugging in the openloop feedback cable. I believe this to be a result of my dodgy leads, since now removing the cable results in the same thing, and prodding and poking wont seem to get my +34dB's back. There is also a marginal difference between the two phase plots.
Enabling the feedback, with the feedback the wrong way around (i.e wires inverted) results in the following gain and phase response
We can see that there appears to be a 2dB reduction in peak gain when plugging in the openloop feedback cable. I believe this to be a result of my dodgy leads, since now removing the cable results in the same thing, and prodding and poking wont seem to get my +34dB's back. There is also a marginal difference between the two phase plots.
Enabling the feedback, with the feedback the wrong way around (i.e wires inverted) results in the following gain and phase response

 With the feedback cable the right way around gives:
With the feedback cable the right way around gives:

 With a 10k feedback resistor, and a flat gain profile for the transformer (x30) and first stage of Squid board amplifier(x500). I expect that the 30*500=15kV/V is strong enough feedback to force the gain of the overall system to: (0.1/50) * (10k/5.1) * 5 *(1/3) = 6.53 => +16.3dB, similarly for the 5k and 3.3k I expect 10.3dB and 6.7dB respectively.
Update - The gain of the transformer and first stage amplifier is 30x500=15000, this is not large enough to assume the gain is totally determined by the resistors. Gfeedback=1/( (5.1/10k) + 1/15e3)=1734 (instead of 1961), therefore we expect 5.78 =>+15.2dB (and similarly for the 5k and 3.3k feed back we get +9.7dB and +6.3dB)
As a check, performing a spice simulation, with a 3.3kOhm feedback resistor and the Squid board amplifier having a bandwidth of 1Mhz gives:
[Note that the x(5/3) is how the differential amplifier and its output resistance was modeled]
* Spice simulation of 3k3 feedback:
With a 10k feedback resistor, and a flat gain profile for the transformer (x30) and first stage of Squid board amplifier(x500). I expect that the 30*500=15kV/V is strong enough feedback to force the gain of the overall system to: (0.1/50) * (10k/5.1) * 5 *(1/3) = 6.53 => +16.3dB, similarly for the 5k and 3.3k I expect 10.3dB and 6.7dB respectively.
Update - The gain of the transformer and first stage amplifier is 30x500=15000, this is not large enough to assume the gain is totally determined by the resistors. Gfeedback=1/( (5.1/10k) + 1/15e3)=1734 (instead of 1961), therefore we expect 5.78 =>+15.2dB (and similarly for the 5k and 3.3k feed back we get +9.7dB and +6.3dB)
As a check, performing a spice simulation, with a 3.3kOhm feedback resistor and the Squid board amplifier having a bandwidth of 1Mhz gives:
[Note that the x(5/3) is how the differential amplifier and its output resistance was modeled]
* Spice simulation of 3k3 feedback:
 In the Spice simulation, at 330kHz, approximately the resonant frequency of the transformer, the overall system gain is +6.1dB which is close to our predicted value and measured value. Interesting the Spice simulation and measured results both have the bump in the response between 1->2 MHz. The measured response 'bump' is about 10db larger than our simulation. Perhaps a single pole at 1Mhz is insufficient.
Note that although we're seeing an overall system gain of 2 with 3.3k feedback, this actually corresponds to a transimpedance of (5.1*50/0.1)*2=5100 Volts/Amp that flows through the bolometer
In the Spice simulation, at 330kHz, approximately the resonant frequency of the transformer, the overall system gain is +6.1dB which is close to our predicted value and measured value. Interesting the Spice simulation and measured results both have the bump in the response between 1->2 MHz. The measured response 'bump' is about 10db larger than our simulation. Perhaps a single pole at 1Mhz is insufficient.
Note that although we're seeing an overall system gain of 2 with 3.3k feedback, this actually corresponds to a transimpedance of (5.1*50/0.1)*2=5100 Volts/Amp that flows through the bolometer


 Looking at the plots, the most noticeable feature is that the Phase on the two channels are inverse with respect to each other. Specifically, Squid channel 1 (unfortunately my transformer) has the wrong polarity. Note that if we really want by playing around with the Squid Control board this can be compensated for, we can unsolder some resistors and put two short wires on, might be worth waiting for things to warm up and just fix it properly though
This data has been matched to simulation by setting the components in the circuit as follows. Note that the gain on the 1:200 transformer seems to provide results that indicate it is a 1:100 transformer. Note also that the 10.8 Ohm resistances have been measured with an Ohm meter, and the 30mOhm resistor is likely to be a 10mOhm resistor instead.
Looking at the plots, the most noticeable feature is that the Phase on the two channels are inverse with respect to each other. Specifically, Squid channel 1 (unfortunately my transformer) has the wrong polarity. Note that if we really want by playing around with the Squid Control board this can be compensated for, we can unsolder some resistors and put two short wires on, might be worth waiting for things to warm up and just fix it properly though
This data has been matched to simulation by setting the components in the circuit as follows. Note that the gain on the 1:200 transformer seems to provide results that indicate it is a 1:100 transformer. Note also that the 10.8 Ohm resistances have been measured with an Ohm meter, and the 30mOhm resistor is likely to be a 10mOhm resistor instead.

 Is is important to note that it is possible to compare the relative gains (independent of the biasing circuitry) of two transformers using the circuit shown above. The 50Ohm load of the spectrum analyzer, when refered to the primary of the transformer, dominates over the reactive components (the magnetising inductance and output capacitance). The gain of the circuit becomes: (Rbias/Rin) * (Rload/N^2)/Rbolo * N = K/N. Given that the same circuitry is used on both Squid channels 1 and 8, the constant K remains the same. So the overall circuit gain is inversely proportional to the transformer gain. We believed that we were using transformers with gain 200 and 300. This corresponds to a 3.5dB difference in gain. We can see on the measured data that we have approximately a 10dB difference in gain. This corresponds to approximately a factor of 3 difference in gain. Assuming that we've correctly worked out what the bias circuitry is, Squid channel 8 appears to fit the measured data, hence Squid channel 1 has a gain of 100.
We will test this further.
Simulating the following spice circuit
* SimSecToPrimGain.jpg:
Is is important to note that it is possible to compare the relative gains (independent of the biasing circuitry) of two transformers using the circuit shown above. The 50Ohm load of the spectrum analyzer, when refered to the primary of the transformer, dominates over the reactive components (the magnetising inductance and output capacitance). The gain of the circuit becomes: (Rbias/Rin) * (Rload/N^2)/Rbolo * N = K/N. Given that the same circuitry is used on both Squid channels 1 and 8, the constant K remains the same. So the overall circuit gain is inversely proportional to the transformer gain. We believed that we were using transformers with gain 200 and 300. This corresponds to a 3.5dB difference in gain. We can see on the measured data that we have approximately a 10dB difference in gain. This corresponds to approximately a factor of 3 difference in gain. Assuming that we've correctly worked out what the bias circuitry is, Squid channel 8 appears to fit the measured data, hence Squid channel 1 has a gain of 100.
We will test this further.
Simulating the following spice circuit
* SimSecToPrimGain.jpg:
 Gives these expected gain results:
* ExpectedSecToPrimGain.jpg:
Gives these expected gain results:
* ExpectedSecToPrimGain.jpg:
 Comparing this with measured data taken after :
* MeasuredPrimSecGains.jpg:
Comparing this with measured data taken after :
* MeasuredPrimSecGains.jpg:
 * MeasuredPrimSecPhase.jpg:
* MeasuredPrimSecPhase.jpg:
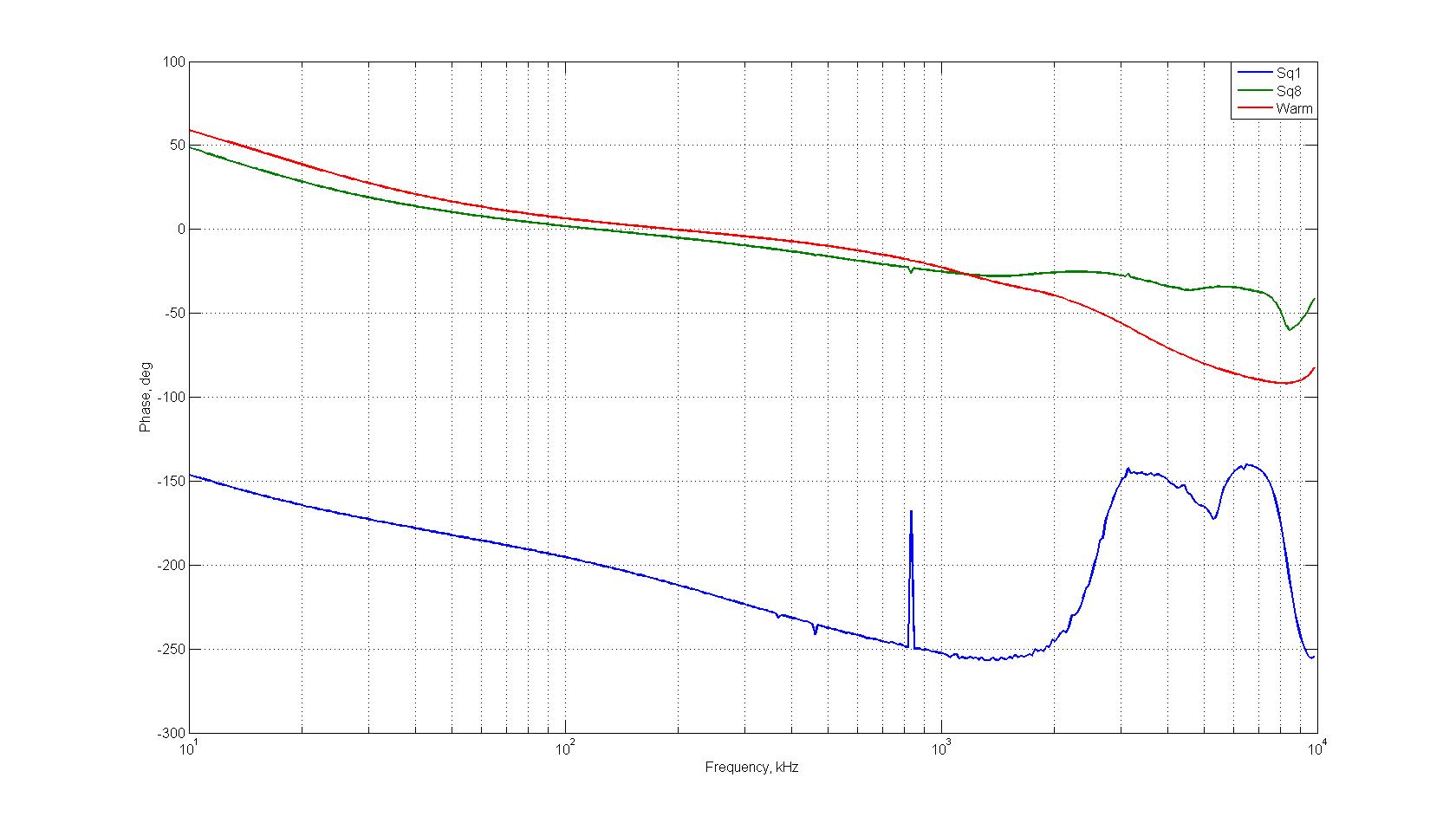 We can see that in the flat parts of the measured results we have the predicted gains for each channel (Note that this measurement is independent of the biasing circuitry, and only depends on the gain of the transformer)
This is conclusive evidence that the Warm transformer has a gain 30, SQ1 has a transformer gain 300 and SQ1 has a transformer gain 100
We can see that in the flat parts of the measured results we have the predicted gains for each channel (Note that this measurement is independent of the biasing circuitry, and only depends on the gain of the transformer)
This is conclusive evidence that the Warm transformer has a gain 30, SQ1 has a transformer gain 300 and SQ1 has a transformer gain 100
 * SQ8ClosedLoopPhase.jpg:
* SQ8ClosedLoopPhase.jpg:
 At present I could not have predicted these results. Note that the Bolobias channels have 400Ohm of resistance in them. This greatly reduces the gain and may need to be changed. We do not know the transformer magnetizing inductance or capacitance. Given a turns ratio of 1:100 and knowing how painful the cores are to wind. Its likely the the primary has between 1 and 3 turns. This limits the inductance to 70nH, 280nH, 630nH. In terms of output capacitance, the 5:154 warm transformer had 10pF on the secondary. Its likely that the 1:100 transformer has a similar capacitance. At most it may have 20pF.
At present I could not have predicted these results. Note that the Bolobias channels have 400Ohm of resistance in them. This greatly reduces the gain and may need to be changed. We do not know the transformer magnetizing inductance or capacitance. Given a turns ratio of 1:100 and knowing how painful the cores are to wind. Its likely the the primary has between 1 and 3 turns. This limits the inductance to 70nH, 280nH, 630nH. In terms of output capacitance, the 5:154 warm transformer had 10pF on the secondary. Its likely that the 1:100 transformer has a similar capacitance. At most it may have 20pF.
 We can see that when the capacitor is included, the usefull bandwidth of the system under feedback is much greater.
We can see that when the capacitor is included, the usefull bandwidth of the system under feedback is much greater.
 * Sq1-Phase.jpg:
* Sq1-Phase.jpg:
 * Sq-NoiseUnfiltered.jpg:
* Sq-NoiseUnfiltered.jpg:

This topic: ColdFeedback > WebHome > ColdTransformerOpampTesting Topic revision: r26 - 2010-02-17 - WinterlandUser
Testing the ADA4817-1ARDZ OpAmp
- Transformers in the cryostat
- Testing the ADA4817-1ARDZ OpAmp
- To Do List
- Pulling data from Spectrum analyzer
- New vs Old Amplifier noise (10 Ohm)
- New vs Old Amplifier noise (10k Ohm)
- Explanation for low frequency behavior
- Noise envelope vs Frequency response
- Lisa Chan 1 - ADA4817 - Frequency response
- Transformer (with matching circuitry) Frequency response
- Future plans
- Problems with squid control board
- Channel 1 and 8 frequency response
- Source of some of the spikes
- Circuit diagram of Transformer with Squid control card
- Squid control board noise measurements
- Antenna test
- Most basic transformer gain test
- Transformer gain test with Squid controller board
- Feedback testing
- Warm Feedback Noise testing
- Cold Openloop Gain testing
- Cold Feedback testing of SQ8
- Squid control board changes
- SQ8 measurements with the above resistance changes and showing how Capacitance on secondary affects results
- Feb 3rd, 2010 - Dewar Measurements
To Do List
Here is a table of the measurements planned to be done on the transformers in the dewar and warm.| Test | Status | Expected Results | Measured Results |
|---|---|---|---|
| Warm Tests | |||
| -- Capacitance Test | Done | Oscillations if unstable | Pass (1nF okay) |
| -- Transformer Gain Test | Not Done - parts available | Expect gain of Gt(=30)*Glb(=835) = 25050 = 88 dB | |
| -- Close feedback for warm transformer | Done | Gain of 6dB | Gain and noise make sense (see below) |
| Dewar Tests | |||
| -- Measure R11/R12 | Not Done - impossible (all lines see 30mOhms) | 1 Ohm where shown in diagram - found two 1 ohms used up | |
| -- Cold Transformer w/ 4195a | Not Done, need to make cables | Need to calculate expected gain using R11/R12 values measured | |
| -- Cold Transformer w/ LISA+4195a | Not Done, need HD62 pin connector | ?? | |
| -- Cold Transformer w/ Mezz | Not Done - all cables available | Need to calculate | |
Pulling data from Spectrum analyzer
* SpectScan2.py.txt: Python code to run n spectrum analyzer sweeps and average the dataNew vs Old Amplifier noise (10 Ohm)
OpAmp datasheet GBP(Gain bandwidth product) and Noise
OPA847 has a GBP of 3.9Ghz and an equivalent voltage noise of 0.85nV/sqrt(Hz) ADA4817 has a GBP of 1Ghz and an equivalent voltage noise of 4nV/sqrt(Hz)Circuit gain, bandwidth & expected output noise levels
The gain of the OpAmp in both cases is 69.8k Ohms /20 Ohms = 3490 This gives a bandwidth of 1.1Ghz for the OPA847 and a bandwidth of 286kHz for the ADA4817 The overall circuit gain is (69.8k/20) * 20/(20+121) * (499/99.66) * (50/150) = 826 (when using a 50 Ohm load) (note that 121//20 + 82.5 = 99.66 Ohms) We therefore expect a noise level of 0.7uV/sqrt(Hz) in the flat region of the OPA847 response and a noise level of 3.3uV/sqrt(Hz) in the flat region of the ADA4817 responseMeasured noise levels with 10Ohm input
With a 10 Ohm resistor between the amplifiers +ve terminal and ground gives the following output noise response on the HP4195A spectrum analyzer: For the ADA4817 and OPA847 an Offset of -0.11 and +0.005 zeroes the differential output respectfully * 50x Averaged noise output , 1kHz resolution bandwidth NoiseNewOld10Ohm.mat: Raw data for figure From the figure the flat noise level of the OPA847 circuit is 1.8uV/sqrt(Hz) and similarly for the ADA4817 there is 5.1uV/sqrt(Hz)
Note that repeating the measurements results in similar figures i.e the spikes in the noise response of the OPA847 are indeed there (690kHz and 6.1Mhz)
* 200x averaged 10kHz resolution bandwidth
NoiseFloor10OhmRB10k.mat: Raw data for 10k Resolution bandwidth figure
From the figure the flat noise level of the OPA847 circuit is 1.8uV/sqrt(Hz) and similarly for the ADA4817 there is 5.1uV/sqrt(Hz)
Note that repeating the measurements results in similar figures i.e the spikes in the noise response of the OPA847 are indeed there (690kHz and 6.1Mhz)
* 200x averaged 10kHz resolution bandwidth
NoiseFloor10OhmRB10k.mat: Raw data for 10k Resolution bandwidth figure
 With a larger resolution bandwidth the spikes in the spectrum can no longer be seen - note also that the low frequency part of the response is more flat
With a larger resolution bandwidth the spikes in the spectrum can no longer be seen - note also that the low frequency part of the response is more flat
New vs Old Amplifier noise (10k Ohm)
The OPA847 rails and cannot be brought back into operation via the offset. The ADA4817 requires a new offset voltage (-2.065V) * 50x Averaged 1kHz resolution bandwidth NoiseFloor10kOhmRB1k.mat: Source data for figure The spikes are now visible on this OpAmp (250kHz,645kHz,690kHz,1.2Mhz ,1.9kHz, 2.2Mhz, 3.8MHz). The spikes are at different frequencies to the previous OPA847.
The noise level is typically 9.1uV/sqrt(Hz) in the pass band
The spikes are now visible on this OpAmp (250kHz,645kHz,690kHz,1.2Mhz ,1.9kHz, 2.2Mhz, 3.8MHz). The spikes are at different frequencies to the previous OPA847.
The noise level is typically 9.1uV/sqrt(Hz) in the pass band
Explanation for low frequency behavior
The transformer that is used to couple the differential output signal to the scope is likely to cause this After looking at transformer response on its own, 1khz is way out of its bandwidth, only data above 10khz is valid.Noise envelope vs Frequency response
* 50x averaged running the ADA4817 on the Lisa board:ADA481gain.mat: Source data for figure
 I currently do not understand why the gain is 1210 at the peak. I was expecting 826 as stated earlier.
Note also that when looking at the noise plots shown earlier, the input noise to the ADA4817 is 4nV/sqrt(Hz) and the output noise of the amplifier is 5.1uV/sqrt(Hz) giving a gain of 1275
Strange...... Have a feeling that the component values on the Lisa board for Channel 1 is not the same as that on the schematic
* Frequency response overlaid with the 10Ohm noise scaled up by 235x:
I currently do not understand why the gain is 1210 at the peak. I was expecting 826 as stated earlier.
Note also that when looking at the noise plots shown earlier, the input noise to the ADA4817 is 4nV/sqrt(Hz) and the output noise of the amplifier is 5.1uV/sqrt(Hz) giving a gain of 1275
Strange...... Have a feeling that the component values on the Lisa board for Channel 1 is not the same as that on the schematic
* Frequency response overlaid with the 10Ohm noise scaled up by 235x:  Note that although the 235x was chosen to visually allow the easiest shape comparison, it can be calculated approximately from 1/( 1e6 x OpAmp input noise)
Note that although the 235x was chosen to visually allow the easiest shape comparison, it can be calculated approximately from 1/( 1e6 x OpAmp input noise)
Lisa Chan 1 - ADA4817 - Frequency response
* LisaFreqResp.mat: Raw data from Lisa Chan 1 frequency response * Lisa Chan1 frequency response (new opamp):
 From the above frequency response data, the gain peaks at +61.7dB giving 1216 V/V with a bandwidth of 350kHz
From the above frequency response data, the gain peaks at +61.7dB giving 1216 V/V with a bandwidth of 350kHz
Transformer (with matching circuitry) Frequency response
The transformer & matching circuitry consists of two 25Ohm resistors at each input terminal, followed by a 0.1 Ohm resistor in series with both the 25Ohms. This gives a 50Ohm input impedance, and forms a potential divider with the 0.1 Ohm. In parallel with the 0.1 Ohm is a 5.1 Ohm resistor (to model the bolometer) in series with the transformer primary (i.e all current flowing through the 5.1 Ohm resistor flows into the transformer primary). On the secondary of the transformer is a 236pF capacitor. The transformer gain is 30 V/V and the primary magnetizing inductance is 1uH. * AdamTrans1FreqResp.mat: Raw data for Transformer frequency response figures * Transformer frequency response:
 I would firstly predict that the resonant frequency is at 1/(2*Pi*sqrt(1uH *236pF*30^2)) = 345kHz, secondly I would predict that the gain at resonance (when the input impedance of the transformer is ideally infinite - think parallel LC) is 0.1/(50.1) i.e the voltage gain is independent of the 5.1Ohm resistor = 30*2e-3V/V => -24.4dB
The graph shows -35dB's we are loosing 10.6dB somewhere. This points to the transformer having a large leakage inductance (bad coupling) , for instance 0.71uH leakage and 0.29uH magnetizing. To improve this, much more windings are required on the primary, and if possible the windings should be directly over each other. Alternatively the peak gain is consistent with a load of 2kOhms present on the secondary - thus forming a divider with the 5.1Ohm. Perhaps we have some combination of these two processes taking place.
Just to be sure that the transformer has been characterized properly. Here are results taken by feeding a 10V p-p signal from the function generator into the transformer(with matching circuitry) for both a 10k load and open load on the transformer secondary. An oscilloscope is used to read both the input and output of the network, both channels being on the 1MOhm input impedance setting. Note that we're getting very close to the predicted transformer gain. This points to some additional loading taking place on the Lisa board at the input to the amplifier i.e I believe that we're having some potential divider going on.
* Transformer (and matching circuitry) frequency response taken by hand:
I would firstly predict that the resonant frequency is at 1/(2*Pi*sqrt(1uH *236pF*30^2)) = 345kHz, secondly I would predict that the gain at resonance (when the input impedance of the transformer is ideally infinite - think parallel LC) is 0.1/(50.1) i.e the voltage gain is independent of the 5.1Ohm resistor = 30*2e-3V/V => -24.4dB
The graph shows -35dB's we are loosing 10.6dB somewhere. This points to the transformer having a large leakage inductance (bad coupling) , for instance 0.71uH leakage and 0.29uH magnetizing. To improve this, much more windings are required on the primary, and if possible the windings should be directly over each other. Alternatively the peak gain is consistent with a load of 2kOhms present on the secondary - thus forming a divider with the 5.1Ohm. Perhaps we have some combination of these two processes taking place.
Just to be sure that the transformer has been characterized properly. Here are results taken by feeding a 10V p-p signal from the function generator into the transformer(with matching circuitry) for both a 10k load and open load on the transformer secondary. An oscilloscope is used to read both the input and output of the network, both channels being on the 1MOhm input impedance setting. Note that we're getting very close to the predicted transformer gain. This points to some additional loading taking place on the Lisa board at the input to the amplifier i.e I believe that we're having some potential divider going on.
* Transformer (and matching circuitry) frequency response taken by hand: 
Future plans
Two transformers have been placed on a squid board in the cryostat. The squid control board that I've been testing has been mounted on the cryostat to read the squid board. 1) We need to use the network analyzer to take initial frequency response data for both transformer channels (Open loop) 2) Repeat 1) for closed loop settings 3) Perform noise measurements for both 1) and 2) 4) Use the DfMux readout system to repeat both steps 1) 2) and 3) 5) Compare DfMux readout system data with spectrum analyzer data, a consistency check 6) Calculate what we should be seeing, compare measured results with calculationProblems with squid control board
It was found that a number of components should be adjusted on the squid control board. Channels 1 and 8 have been adjusted as follows:- Cx04 was ensured to be open - (it was)
- Rx22 was removed
- Rx25 was replaced with a 10k resistor (from 69.8k)
- Rx24 was replaced with a 0 Ohm resistor (from 121 Ohms)
- Rx23 was removed (from 20 Ohms)
- Rx15 was replaced with 100 Ohms (from 82.5 Ohms)
- Rx21 and Rx72 were replaced (from 2k each) to 499 Ohms
- Just in case it becomes important, note that there is a 21k resistance between the two output pins of the Diff amp. This is part of the amplifier IC.
- Additionally Cx17, Cx20, Rx34 and Rx40 have been removed. This disconnects the squid out pins on the DB37 connector from the Squid out pins on the 3 row connector
- 1/ MeasuredOpampCircuitGain =1/ OpenLoopOpampGain +1/ IdealOpampCircuitGain
- 1/410.4=1/X+1/500
- X=2290
Channel 1 and 8 frequency response
Using the spectrum analyzer the following data has been captured for both channels 1 and 8. * Chan1Chan8data2.mat: Frequency response data for Chan1 and Chan8 * Chan1Chan8FSweep.jpg: * Chan1Chan8FSweepPhase.jpg:
* Chan1Chan8FSweepPhase.jpg:  The bandwidth on both channels appears to be approximately 950kHz. This is smaller than the expected 2Mhz, calculated from the 1GHz bandwidth and circuit gain of 500.
Even through the the open loop gain of the amplifier is low, from see p.2 http://users.ece.gatech.edu/mleach/ece3050/notes/OpAmps/opampbw.pdf or the attached file opampbw.pdf the gain bandwidth product should still hold.
Additionally the drop of rate is approximately -20dB/decade which is consistant with a first order amplifier.
The bandwidth on both channels appears to be approximately 950kHz. This is smaller than the expected 2Mhz, calculated from the 1GHz bandwidth and circuit gain of 500.
Even through the the open loop gain of the amplifier is low, from see p.2 http://users.ece.gatech.edu/mleach/ece3050/notes/OpAmps/opampbw.pdf or the attached file opampbw.pdf the gain bandwidth product should still hold.
Additionally the drop of rate is approximately -20dB/decade which is consistant with a first order amplifier.
Source of some of the spikes
The spikes appear as a direct result of having the GPIB cable plugged into the back of the spectrum analyzer, with the cable out we don't have spikes. Update: We still see spikes but at lower amplitudes.Circuit diagram of Transformer with Squid control card
 *VBolo- is grounded via one of the feedback lines *
*VBolo- is grounded via one of the feedback lines *
Squid control board noise measurements
RBW=1kHz, and 20 averages are taken. Placing a resistor, 0Ohms, 1k and 10k as closely as possible to the input header of the Squid control board results in the following noise data on Channels 1 and 8. Note that the vertical axis is uV/sqrt(Hz). An additional curve is plotted on each figure, this curve corresponds to that channels measured gain vs frequency. This was provides a few sections earlier on this Wikipage. Note that the scaling factor on the gain is 1/200. I.e Multiplying 4uV/sqrt(Hz) on the vertical axis by 200 sqrt(Hz)/uV, results in a gain of 800. * Chan1 Noise vs R: * Chan8 Noise vs R:
* Chan8 Noise vs R:  The noise measurements in the flat regions of the above figures are consistent with that expected.
For a 0Ohm load, the expected noise is 835 x 4nV/sqrt(Hz) = 3.3uV/sqrt(Hz)
For a 1kOhm load, the expected noise is as follows:
Noise=sqrt(4*Kb*T*R)=0.13*Sqrt(R) nV/sqrt(Hz) = 4.1nV/sqrt(Hz) at 300k. The amplifier noise is 4nV/sqrt(Hz) which adds in quadrature. The total expected noise is therefore 5.7nV*835=4.8uV/sqrt(Hz)
For a 10kOhm load the expected noise is:
13nV/sqrt(Hz) in quadrature with 4nV/sqrt(Hz), multiplied by 835 = 11.4uV/sqrt(Hz)
Note that the noise Spikes seen at 830kHz are not related to the GPIB and we believe them to be radio based
The noise measurements in the flat regions of the above figures are consistent with that expected.
For a 0Ohm load, the expected noise is 835 x 4nV/sqrt(Hz) = 3.3uV/sqrt(Hz)
For a 1kOhm load, the expected noise is as follows:
Noise=sqrt(4*Kb*T*R)=0.13*Sqrt(R) nV/sqrt(Hz) = 4.1nV/sqrt(Hz) at 300k. The amplifier noise is 4nV/sqrt(Hz) which adds in quadrature. The total expected noise is therefore 5.7nV*835=4.8uV/sqrt(Hz)
For a 10kOhm load the expected noise is:
13nV/sqrt(Hz) in quadrature with 4nV/sqrt(Hz), multiplied by 835 = 11.4uV/sqrt(Hz)
Note that the noise Spikes seen at 830kHz are not related to the GPIB and we believe them to be radio based
Antenna test
To compare the locations of the noise spikes with radiated noise in the lab, the bow tie antenna is used as an input to the Squid control board amplifier and a noise measurement performed on the spectrum analyzer. Note that substantially more noise is picked up when the antenna is vertical, which could be a result of the vertical GPIB cable? * Antenna noise:
Most basic transformer gain test
In the diagram we see two virtually identical spice configurations for the experimental setup. The spice simulation data for these two configurations can be seen in the following figure:
The spice simulation data for these two configurations can be seen in the following figure:
 The spectrum analyzer measurements are as follows:
The spectrum analyzer measurements are as follows:
 Interestingly the spice configuration with the 15nH inductance in series with the 0.1Ohm bias resistor provides the most accurate model.
Interestingly the spice configuration with the 15nH inductance in series with the 0.1Ohm bias resistor provides the most accurate model.
Transformer gain test with Squid controller board
The warm transformer with transformer ratio 1:30 (5:154) @ 42nH/turn^2 is used as an input stage to the Squid control board amplifier. * Warm transformer stage circuit diagram: Using the above circuit as a front end to the Squid control board amplifier should result in a peak gain, at a resonant frequency of f=1/(2*Pi*sqrt(1mH*236pF))=328kHz. Note that the 1mH in the calculation is the reflected value of the primary inductance to the secondary. The gain, at that resonant frequency is expected to be 20log( (0.1/50)*30*835 )=+34dB. Note that the 0.1/50 corresponds to the potential divider at the front of the transformer stage and the 30 corresponds to the transformer voltage gain. At resonance the reactive components (since they are in parallel) have 'infinite' impedance and hence disappear from the calculation.
Testing the system frequency response on the Spectrum analyzer results in the following figures.
* Gain vs Frequency for Transformer and Squid control board amplifier:
Using the above circuit as a front end to the Squid control board amplifier should result in a peak gain, at a resonant frequency of f=1/(2*Pi*sqrt(1mH*236pF))=328kHz. Note that the 1mH in the calculation is the reflected value of the primary inductance to the secondary. The gain, at that resonant frequency is expected to be 20log( (0.1/50)*30*835 )=+34dB. Note that the 0.1/50 corresponds to the potential divider at the front of the transformer stage and the 30 corresponds to the transformer voltage gain. At resonance the reactive components (since they are in parallel) have 'infinite' impedance and hence disappear from the calculation.
Testing the system frequency response on the Spectrum analyzer results in the following figures.
* Gain vs Frequency for Transformer and Squid control board amplifier:  * Phase vs Frequency for Transformer and Squid control board amplifier:
* Phase vs Frequency for Transformer and Squid control board amplifier:  It can be seen from the measured frequency response that the peak gain and associated frequency are as expected.
It can be seen from the measured frequency response that the peak gain and associated frequency are as expected.
Feedback testing
The feedback wires are attached, and the gain of the system measured to check for any differences. * Sytem Gain with feedback wires connected - Resistance=Open: * WarmFeedbackPhaseOpen.jpg:
* WarmFeedbackPhaseOpen.jpg:  We can see that there appears to be a 2dB reduction in peak gain when plugging in the openloop feedback cable. I believe this to be a result of my dodgy leads, since now removing the cable results in the same thing, and prodding and poking wont seem to get my +34dB's back. There is also a marginal difference between the two phase plots.
Enabling the feedback, with the feedback the wrong way around (i.e wires inverted) results in the following gain and phase response
We can see that there appears to be a 2dB reduction in peak gain when plugging in the openloop feedback cable. I believe this to be a result of my dodgy leads, since now removing the cable results in the same thing, and prodding and poking wont seem to get my +34dB's back. There is also a marginal difference between the two phase plots.
Enabling the feedback, with the feedback the wrong way around (i.e wires inverted) results in the following gain and phase response

 With the feedback cable the right way around gives:
With the feedback cable the right way around gives:

 With a 10k feedback resistor, and a flat gain profile for the transformer (x30) and first stage of Squid board amplifier(x500). I expect that the 30*500=15kV/V is strong enough feedback to force the gain of the overall system to: (0.1/50) * (10k/5.1) * 5 *(1/3) = 6.53 => +16.3dB, similarly for the 5k and 3.3k I expect 10.3dB and 6.7dB respectively.
Update - The gain of the transformer and first stage amplifier is 30x500=15000, this is not large enough to assume the gain is totally determined by the resistors. Gfeedback=1/( (5.1/10k) + 1/15e3)=1734 (instead of 1961), therefore we expect 5.78 =>+15.2dB (and similarly for the 5k and 3.3k feed back we get +9.7dB and +6.3dB)
As a check, performing a spice simulation, with a 3.3kOhm feedback resistor and the Squid board amplifier having a bandwidth of 1Mhz gives:
[Note that the x(5/3) is how the differential amplifier and its output resistance was modeled]
* Spice simulation of 3k3 feedback:
With a 10k feedback resistor, and a flat gain profile for the transformer (x30) and first stage of Squid board amplifier(x500). I expect that the 30*500=15kV/V is strong enough feedback to force the gain of the overall system to: (0.1/50) * (10k/5.1) * 5 *(1/3) = 6.53 => +16.3dB, similarly for the 5k and 3.3k I expect 10.3dB and 6.7dB respectively.
Update - The gain of the transformer and first stage amplifier is 30x500=15000, this is not large enough to assume the gain is totally determined by the resistors. Gfeedback=1/( (5.1/10k) + 1/15e3)=1734 (instead of 1961), therefore we expect 5.78 =>+15.2dB (and similarly for the 5k and 3.3k feed back we get +9.7dB and +6.3dB)
As a check, performing a spice simulation, with a 3.3kOhm feedback resistor and the Squid board amplifier having a bandwidth of 1Mhz gives:
[Note that the x(5/3) is how the differential amplifier and its output resistance was modeled]
* Spice simulation of 3k3 feedback:  In the Spice simulation, at 330kHz, approximately the resonant frequency of the transformer, the overall system gain is +6.1dB which is close to our predicted value and measured value. Interesting the Spice simulation and measured results both have the bump in the response between 1->2 MHz. The measured response 'bump' is about 10db larger than our simulation. Perhaps a single pole at 1Mhz is insufficient.
Note that although we're seeing an overall system gain of 2 with 3.3k feedback, this actually corresponds to a transimpedance of (5.1*50/0.1)*2=5100 Volts/Amp that flows through the bolometer
In the Spice simulation, at 330kHz, approximately the resonant frequency of the transformer, the overall system gain is +6.1dB which is close to our predicted value and measured value. Interesting the Spice simulation and measured results both have the bump in the response between 1->2 MHz. The measured response 'bump' is about 10db larger than our simulation. Perhaps a single pole at 1Mhz is insufficient.
Note that although we're seeing an overall system gain of 2 with 3.3k feedback, this actually corresponds to a transimpedance of (5.1*50/0.1)*2=5100 Volts/Amp that flows through the bolometer
Warm Feedback Noise testing
Here we take noise measurements for the transformer with Squid control board amplifier. Note that for simplicity all the measurements are placed on the same plot. The noise floor of the spectrum analyzer is approximately 1uV/sqrt(Hz) (the spectrum analyzer was set to 30dB attenuation and 100Hz RBW). Open loop noise: I expect the largest noise to occur at resonance since the reactive components are performing no attenuation at this point. Vnoise= (0.13*sqrt(5.2 Ohms)) * 30 = 8.9nV/sqrt(Hz) due to the 5.1Ohm resistor in series with the 0.1Ohm resistor at the primary of the transformer. This adds in quadrature with the front end amplifier noise =4nV/sqrt(Hz) which gives a total of 9.8nV/sqrt(Hz). Scaling this by the amplifier gains gives 9.8nV/sqrt(Hz) * 500 * 5/3=8130nV/sqrt(Hz) = 8.1uV/sqrt(Hz). The measured data I would say has a peak noise level of around 12uV/sqrt(Hz) (when you mentally try and plot a line of best fit). The slightly higher level may be due to the transformer winding resistance on the primary which is approximately 0.5Ohms. Factoring this into account gives: 8.4uV/sqrt(Hz). We have slightly more noise than we expect. Closed loop: This is very interesting, when the gain of the transformer is at its minimum, i.e at very low and high frequency, the overall system noise is equivalent to the open-loop case. When the gain of the transformer is a maximum, i.e at its 330kHz resonance, the noise level falls to the spectrum analyzer noise floor. Closing the loop greatly reduces the noise level, with respect to the open loop noise, at the resonant frequency of the transformer. Interestingly we see the noise level lift between 1->2Mhz (around the peaking previously reported in the closed loop frequency response). Note that I have not shown data for the 3.3k Ohm feedback case, the noise greatly lifts across the whole band and causes the Spectrum analyzer to overload. Increasing the attenuation further will greatly increase the noise floor making it difficult to know what belongs to the spectrum analyzer noise and what belongs to the amplifier. * WarmTransFeedback.jpg:
Cold Openloop Gain testing
For SQ1 feeding a signal from the spectrum analyzer into the BoloBias pins 36 and 18 (ground), and looking at the SquidOut pins 35 and 17(ground) For SQ8 feeding a signal from the spectrum analyzer into the BoloBias pins 22 and 4 (ground), and looking at the SquidOut pins 21 and 3(ground) The following results are obtained:
 Looking at the plots, the most noticeable feature is that the Phase on the two channels are inverse with respect to each other. Specifically, Squid channel 1 (unfortunately my transformer) has the wrong polarity. Note that if we really want by playing around with the Squid Control board this can be compensated for, we can unsolder some resistors and put two short wires on, might be worth waiting for things to warm up and just fix it properly though
This data has been matched to simulation by setting the components in the circuit as follows. Note that the gain on the 1:200 transformer seems to provide results that indicate it is a 1:100 transformer. Note also that the 10.8 Ohm resistances have been measured with an Ohm meter, and the 30mOhm resistor is likely to be a 10mOhm resistor instead.
Looking at the plots, the most noticeable feature is that the Phase on the two channels are inverse with respect to each other. Specifically, Squid channel 1 (unfortunately my transformer) has the wrong polarity. Note that if we really want by playing around with the Squid Control board this can be compensated for, we can unsolder some resistors and put two short wires on, might be worth waiting for things to warm up and just fix it properly though
This data has been matched to simulation by setting the components in the circuit as follows. Note that the gain on the 1:200 transformer seems to provide results that indicate it is a 1:100 transformer. Note also that the 10.8 Ohm resistances have been measured with an Ohm meter, and the 30mOhm resistor is likely to be a 10mOhm resistor instead.

 Is is important to note that it is possible to compare the relative gains (independent of the biasing circuitry) of two transformers using the circuit shown above. The 50Ohm load of the spectrum analyzer, when refered to the primary of the transformer, dominates over the reactive components (the magnetising inductance and output capacitance). The gain of the circuit becomes: (Rbias/Rin) * (Rload/N^2)/Rbolo * N = K/N. Given that the same circuitry is used on both Squid channels 1 and 8, the constant K remains the same. So the overall circuit gain is inversely proportional to the transformer gain. We believed that we were using transformers with gain 200 and 300. This corresponds to a 3.5dB difference in gain. We can see on the measured data that we have approximately a 10dB difference in gain. This corresponds to approximately a factor of 3 difference in gain. Assuming that we've correctly worked out what the bias circuitry is, Squid channel 8 appears to fit the measured data, hence Squid channel 1 has a gain of 100.
We will test this further.
Simulating the following spice circuit
* SimSecToPrimGain.jpg:
Is is important to note that it is possible to compare the relative gains (independent of the biasing circuitry) of two transformers using the circuit shown above. The 50Ohm load of the spectrum analyzer, when refered to the primary of the transformer, dominates over the reactive components (the magnetising inductance and output capacitance). The gain of the circuit becomes: (Rbias/Rin) * (Rload/N^2)/Rbolo * N = K/N. Given that the same circuitry is used on both Squid channels 1 and 8, the constant K remains the same. So the overall circuit gain is inversely proportional to the transformer gain. We believed that we were using transformers with gain 200 and 300. This corresponds to a 3.5dB difference in gain. We can see on the measured data that we have approximately a 10dB difference in gain. This corresponds to approximately a factor of 3 difference in gain. Assuming that we've correctly worked out what the bias circuitry is, Squid channel 8 appears to fit the measured data, hence Squid channel 1 has a gain of 100.
We will test this further.
Simulating the following spice circuit
* SimSecToPrimGain.jpg:  Gives these expected gain results:
* ExpectedSecToPrimGain.jpg:
Gives these expected gain results:
* ExpectedSecToPrimGain.jpg:  Comparing this with measured data taken after :
* MeasuredPrimSecGains.jpg:
Comparing this with measured data taken after :
* MeasuredPrimSecGains.jpg:  * MeasuredPrimSecPhase.jpg:
* MeasuredPrimSecPhase.jpg:  We can see that in the flat parts of the measured results we have the predicted gains for each channel (Note that this measurement is independent of the biasing circuitry, and only depends on the gain of the transformer)
This is conclusive evidence that the Warm transformer has a gain 30, SQ1 has a transformer gain 300 and SQ1 has a transformer gain 100
We can see that in the flat parts of the measured results we have the predicted gains for each channel (Note that this measurement is independent of the biasing circuitry, and only depends on the gain of the transformer)
This is conclusive evidence that the Warm transformer has a gain 30, SQ1 has a transformer gain 300 and SQ1 has a transformer gain 100
Cold Feedback testing of SQ8
Measurement data for Squid channel 8, the 1:100 transformer is as follows: * SQ8ClosedLoop.jpg: * SQ8ClosedLoopPhase.jpg:
* SQ8ClosedLoopPhase.jpg:  At present I could not have predicted these results. Note that the Bolobias channels have 400Ohm of resistance in them. This greatly reduces the gain and may need to be changed. We do not know the transformer magnetizing inductance or capacitance. Given a turns ratio of 1:100 and knowing how painful the cores are to wind. Its likely the the primary has between 1 and 3 turns. This limits the inductance to 70nH, 280nH, 630nH. In terms of output capacitance, the 5:154 warm transformer had 10pF on the secondary. Its likely that the 1:100 transformer has a similar capacitance. At most it may have 20pF.
At present I could not have predicted these results. Note that the Bolobias channels have 400Ohm of resistance in them. This greatly reduces the gain and may need to be changed. We do not know the transformer magnetizing inductance or capacitance. Given a turns ratio of 1:100 and knowing how painful the cores are to wind. Its likely the the primary has between 1 and 3 turns. This limits the inductance to 70nH, 280nH, 630nH. In terms of output capacitance, the 5:154 warm transformer had 10pF on the secondary. Its likely that the 1:100 transformer has a similar capacitance. At most it may have 20pF.
Squid control board changes
The Squid board resistors on Channel 1 and 8 have been changed for the Squid Bias. There is now a total resistance of 41 Ohms on the Squid board. This 41 Ohms feeds 10.7, so the total is now 51.7 Ohms.SQ8 measurements with the above resistance changes and showing how Capacitance on secondary affects results
A capacitor 240pF (the same value used on the warm transformer) temporarily is connected from the Non inverting terminal of the Opamp to ground. The following figures show the gain before and after adding the capacitor. * ComparingGainsWithWithoutCap.jpg: We can see that when the capacitor is included, the usefull bandwidth of the system under feedback is much greater.
We can see that when the capacitor is included, the usefull bandwidth of the system under feedback is much greater.
Feb 3rd, 2010 - Dewar Measurements
Tested Squid Channel 1 transformer in cryostat using modified LISA board. Configuration? * Sq1-Gain.jpg: * Sq1-Phase.jpg:
* Sq1-Phase.jpg:  * Sq-NoiseUnfiltered.jpg:
* Sq-NoiseUnfiltered.jpg: 
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
ADA481gain.mat | manage | 17.2 K | 2009-12-10 - 19:13 | WinterlandUser | Raw data for ADA418 gain plot on Lisa board |
| |
AdamTrans1FreqResp.mat | manage | 8.3 K | 2009-12-11 - 18:48 | WinterlandUser | Raw data for Transformer frequency response figures |
| |
AdamTransGain.jpg | manage | 50.8 K | 2009-12-11 - 18:48 | WinterlandUser | Transformer frequency response |
| |
AdamTransPhase.jpg | manage | 48.8 K | 2009-12-11 - 18:49 | WinterlandUser | |
| |
AntNoise.jpg | manage | 137.9 K | 2010-01-28 - 16:57 | WinterlandUser | Antenna noise |
| |
BasicTransTestMeasurments.jpg | manage | 163.3 K | 2010-01-29 - 19:10 | WinterlandUser | |
| |
BasicTransTestSpice.jpg | manage | 43.4 K | 2010-01-29 - 18:55 | WinterlandUser | |
| |
Chan1Chan8FSweep.jpg | manage | 94.2 K | 2010-01-19 - 17:23 | WinterlandUser | |
| |
Chan1Chan8FSweepPhase.jpg | manage | 87.5 K | 2010-01-19 - 17:51 | WinterlandUser | |
| |
Chan1Chan8data.mat | manage | 15.7 K | 2010-01-19 - 17:24 | WinterlandUser | Data for figure |
| |
Chan1Chan8data2.mat | manage | 24.9 K | 2010-01-19 - 17:51 | WinterlandUser | Frequency response data for Chan1 and Chan8 |
| |
Chan1NoisevsR.jpg | manage | 292.0 K | 2010-01-26 - 21:26 | WinterlandUser | |
| |
Chan8NoisevsR.jpg | manage | 290.0 K | 2010-01-26 - 21:30 | WinterlandUser | CHan8 Noise vs R |
| |
ColdCircuitSim1.jpg | manage | 27.0 K | 2010-02-02 - 15:14 | WinterlandUser | |
| |
ComparingGainsWithWithoutCap.jpg | manage | 179.4 K | 2010-02-02 - 21:19 | WinterlandUser | |
| |
ExpectedColdCircuitGainPhase.jpg | manage | 172.0 K | 2010-02-02 - 15:14 | WinterlandUser | |
| |
ExpectedSecToPrimGain.jpg | manage | 174.3 K | 2010-02-02 - 15:41 | WinterlandUser | |
| |
FeedBack3k3Spice.jpg | manage | 150.0 K | 2010-01-29 - 16:31 | WinterlandUser | Spice simulation of 3k3 feedback |
| |
FeedBack3k3SpiceVer2.jpg | manage | 150.0 K | 2010-01-29 - 16:34 | WinterlandUser | Spice simulation of 3k3 feedback |
| |
FeedBack3k3SpiceVer3.jpg | manage | 146.6 K | 2010-01-29 - 16:35 | WinterlandUser | Spice simulation of 3k3 feedback |
| |
FeedbackBad10kAmp.jpg | manage | 147.1 K | 2010-01-28 - 18:22 | WinterlandUser | Bad feedback 10k |
| |
FeedbackBad10kPhase.jpg | manage | 155.5 K | 2010-01-28 - 18:24 | WinterlandUser | |
| |
InductanceOfBiasResistor.jpg | manage | 145.2 K | 2010-01-29 - 18:56 | WinterlandUser | |
| |
LisaFreqResp.mat | manage | 16.0 K | 2009-12-11 - 18:18 | WinterlandUser | Raw data from Lisa Chan 1 frequency response |
| |
LisaGain.jpg | manage | 47.9 K | 2009-12-11 - 18:16 | WinterlandUser | Lisa Chan1 frequency response (new opamp) |
| |
LisaPhase.jpg | manage | 45.3 K | 2009-12-11 - 18:29 | WinterlandUser | CompareBothOpAmpNoise10Ohms |
| |
MeasuredPrimSecGains.jpg | manage | 149.9 K | 2010-02-02 - 16:04 | WinterlandUser | |
| |
MeasuredPrimSecPhase.jpg | manage | 157.5 K | 2010-02-02 - 16:04 | WinterlandUser | |
| |
NewAmpGain.jpg | manage | 88.2 K | 2009-12-10 - 19:10 | WinterlandUser | Running the ADA4817 on the Lisa board |
| |
NoiseFloor10Ohm.mat | manage | 11.1 K | 2009-12-08 - 17:08 | WinterlandUser | Raw data for figure |
| |
NoiseFloor10OhmRB10k.mat | manage | 16.6 K | 2009-12-08 - 19:36 | WinterlandUser | Raw data for 10k Resolution bandiwidth figure |
| |
NoiseFloor10kOhmRB1k.mat | manage | 5.6 K | 2009-12-08 - 20:44 | WinterlandUser | 50x averaged noise output 1k res bandwidth |
| |
NoiseNew10kOhmRB1k.jpg | manage | 66.0 K | 2009-12-08 - 20:43 | WinterlandUser | 50x Averaged noise output 1k res bandwidth |
| |
NoiseNewOld10Ohm.jpg | manage | 60.4 K | 2009-12-08 - 18:16 | WinterlandUser | CompareBothOpAmpNoise10Ohms |
| |
NoiseNewOld10Ohm.mat | manage | 11.0 K | 2009-12-08 - 18:19 | WinterlandUser | Raw data for figure |
| |
NoiseNewOld10OhmBW10k.jpg | manage | 59.3 K | 2009-12-08 - 19:35 | WinterlandUser | 200x averaged 10kHz resolution bandwidh |
| |
NoiseandFreqresp.jpg | manage | 96.7 K | 2009-12-10 - 19:25 | WinterlandUser | Frequency response overlaid with the 10Ohm noise scaled up by 235x |
| |
SQ18Gains.jpg | manage | 156.8 K | 2010-02-02 - 14:57 | WinterlandUser | |
| |
SQ18Phases.jpg | manage | 155.2 K | 2010-02-02 - 14:58 | WinterlandUser | |
| |
SQ8ClosedLoop.jpg | manage | 183.9 K | 2010-02-02 - 19:23 | WinterlandUser | |
| |
SQ8ClosedLoopPhase.jpg | manage | 200.1 K | 2010-02-02 - 19:24 | WinterlandUser | |
| |
SimSecToPrimGain.jpg | manage | 49.5 K | 2010-02-02 - 15:42 | WinterlandUser | |
| |
SpectScan2.py.txt | manage | 1.5 K | 2009-12-08 - 19:40 | WinterlandUser | Python code to run n spectrum analyser sweeps and average the data |
| |
Sq-NoiseUnfiltered.jpg | manage | 138.9 K | 2010-02-17 - 16:24 | WinterlandUser | |
| |
Sq1-Gain.jpg | manage | 101.1 K | 2010-02-17 - 16:23 | WinterlandUser | |
| |
Sq1-Phase.jpg | manage | 106.2 K | 2010-02-17 - 16:23 | WinterlandUser | |
| |
TransFreqResp1.jpg | manage | 51.1 K | 2009-12-11 - 17:18 | WinterlandUser | Frequency response of 1:300 transformer wound by Adam |
| |
TransFreqRespHand.jpg | manage | 40.3 K | 2009-12-15 - 16:56 | WinterlandUser | Transformer (and matching circuitry) frequency response taken by hand |
| |
TransSquidBoardAmp.jpg | manage | 149.9 K | 2010-01-28 - 17:17 | WinterlandUser | Gain vs Frequency for Transformer and Squid control board amplifier |
| |
TransSquidBoardPhase.jpg | manage | 136.5 K | 2010-01-28 - 17:18 | WinterlandUser | Phase vs Frequency for Transformer and Squid control board amplifier |
| |
TransformerStageCircuitDiagram.jpg | manage | 12.4 K | 2010-01-28 - 17:15 | WinterlandUser | Warm transformer stage circuit diagram |
| |
TransformerWithSquidControlCard.jpg | manage | 61.4 K | 2010-01-27 - 17:18 | WinterlandUser | Circuit diagram of Transformer with Squid control card |
| |
TransformerWithSquidControlCard2.jpg | manage | 69.0 K | 2010-01-29 - 19:16 | WinterlandUser | |
| |
WarmFeedbackAmp.jpg | manage | 153.9 K | 2010-01-28 - 18:24 | WinterlandUser | |
| |
WarmFeedbackAmpOpen.jpg | manage | 144.8 K | 2010-01-28 - 17:30 | WinterlandUser | Sytem Gain with feedback wires connected - Resistance=Open |
| |
WarmFeedbackPhase.jpg | manage | 161.8 K | 2010-01-28 - 18:24 | WinterlandUser | |
| |
WarmFeedbackPhaseOpen.jpg | manage | 136.3 K | 2010-01-28 - 18:19 | WinterlandUser | |
| |
WarmFeedbackPhaseUnwraped.jpg | manage | 160.3 K | 2010-01-29 - 16:47 | WinterlandUser | Warm feedback phase |
| |
WarmTransFeedback.jpg | manage | 286.0 K | 2010-02-01 - 18:11 | WinterlandUser | |
| |
WarmTransNoiseWithFeedback.jpg | manage | 317.2 K | 2010-02-01 - 16:00 | WinterlandUser | |
| |
opampbw.pdf | manage | 135.6 K | 2010-01-19 - 16:36 | WinterlandUser | Opamp bandwith analysis |
This topic: ColdFeedback > WebHome > ColdTransformerOpampTesting Topic revision: r26 - 2010-02-17 - WinterlandUser
© 2020 Winterland Cosmology Lab, McGill University, Montréal, Québec, Canada

