---+ Strong Electrothermal Feedback
 The arctan function will do for now. The { R , T } closure relation is then:
%BEGINLATEX%
\begin{equation}
\frac{R}{1 \Omega} = \frac{1}{2} + \frac{1}{\pi} \mathrm{arctan}\left( \frac{T-T_c}{T_0} \right)
\end{equation}
%ENDLATEX%
where T0 is some parameter determining the steepness of the slope.
Or choosing to work in terms of resistance, we can solve for T in order to substitute it into the { P , R , T } relation.
%BEGINLATEX%
\[
T = T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right)
\]
%ENDLATEX%
Substituting:
%BEGINLATEX%
\begin{equation}
\mathrm{Low Pass} \left( P_{sky} + \frac{V_{bias}^2}{R} \right) = G \left[T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right) \right]
\end{equation}
%ENDLATEX%
This equation has no closed form for R. Two options are:
The arctan function will do for now. The { R , T } closure relation is then:
%BEGINLATEX%
\begin{equation}
\frac{R}{1 \Omega} = \frac{1}{2} + \frac{1}{\pi} \mathrm{arctan}\left( \frac{T-T_c}{T_0} \right)
\end{equation}
%ENDLATEX%
where T0 is some parameter determining the steepness of the slope.
Or choosing to work in terms of resistance, we can solve for T in order to substitute it into the { P , R , T } relation.
%BEGINLATEX%
\[
T = T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right)
\]
%ENDLATEX%
Substituting:
%BEGINLATEX%
\begin{equation}
\mathrm{Low Pass} \left( P_{sky} + \frac{V_{bias}^2}{R} \right) = G \left[T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right) \right]
\end{equation}
%ENDLATEX%
This equation has no closed form for R. Two options are:

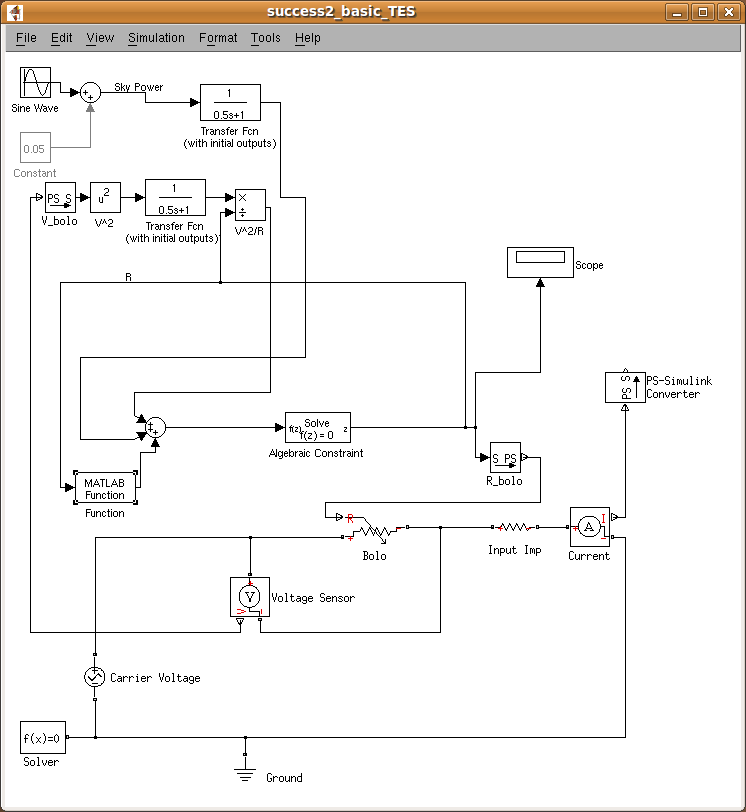 where the "Scope" looks at the bolometer resistance. Varying the strength of the sky signal results in the following plots.
where the "Scope" looks at the bolometer resistance. Varying the strength of the sky signal results in the following plots.


 So the bias voltage is keeping the TES at R >= 0.5 and the sky signal can linearly alter the resistance up to R >> 0.5 where the TES saturates at R = 1.
So the bias voltage is keeping the TES at R >= 0.5 and the sky signal can linearly alter the resistance up to R >> 0.5 where the TES saturates at R = 1.
 Note the inverse relation between I-V at low voltages, the turnaround and the linear behaviour when the bolometer resistance saturates at 1 Ohm. At the lowest voltages, the input impedance of the current meter takes over and the relation becomes linear at a resistance of 0.1 Ohm + Rbolo ( T = 0 )
The feature at the high V end of the plot is an artifact (from when I started the simulation).
Note the inverse relation between I-V at low voltages, the turnaround and the linear behaviour when the bolometer resistance saturates at 1 Ohm. At the lowest voltages, the input impedance of the current meter takes over and the relation becomes linear at a resistance of 0.1 Ohm + Rbolo ( T = 0 )
The feature at the high V end of the plot is an artifact (from when I started the simulation).

 The I_*_V = const part of the curve is the interesting part, since that is where the power applied to the bolometer is constant. For large input impedances, the curve deviates from I_*_V = const behaviour. That deviation implies deviation from strong electrothermal feedback.
-Tijmen
The I_*_V = const part of the curve is the interesting part, since that is where the power applied to the bolometer is constant. For large input impedances, the curve deviates from I_*_V = const behaviour. That deviation implies deviation from strong electrothermal feedback.
-Tijmen
This topic: ColdFeedback > WebHome > StrongElectrothermalFeedback Topic revision: r9 - 2011-11-17 - TijmenDeHaan
Introduction
I am trying to simulate a bolometer using Simulink (an addon to MATLAB). I start from equation (3.6) in Trevor's thesis, which can schematically be written as. (I'm not sure about the derivative and I make some assumptions about G=const) %BEGINLATEX% \begin{equation} \left( P_{sky} + \frac{V_{bias}^2}{R} \right) \frac{1}{1 + i \omega \tau}= G \Delta T \end{equation} %ENDLATEX% where G and C are constants and all other variables can change with time. So this equation gives a way to relate inputs Psky and Vbias to temperature T and TES resistance R. An additional equation relating R to T is required: the shape of the transition. The arctan function will do for now. The { R , T } closure relation is then:
%BEGINLATEX%
\begin{equation}
\frac{R}{1 \Omega} = \frac{1}{2} + \frac{1}{\pi} \mathrm{arctan}\left( \frac{T-T_c}{T_0} \right)
\end{equation}
%ENDLATEX%
where T0 is some parameter determining the steepness of the slope.
Or choosing to work in terms of resistance, we can solve for T in order to substitute it into the { P , R , T } relation.
%BEGINLATEX%
\[
T = T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right)
\]
%ENDLATEX%
Substituting:
%BEGINLATEX%
\begin{equation}
\mathrm{Low Pass} \left( P_{sky} + \frac{V_{bias}^2}{R} \right) = G \left[T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right) \right]
\end{equation}
%ENDLATEX%
This equation has no closed form for R. Two options are:
The arctan function will do for now. The { R , T } closure relation is then:
%BEGINLATEX%
\begin{equation}
\frac{R}{1 \Omega} = \frac{1}{2} + \frac{1}{\pi} \mathrm{arctan}\left( \frac{T-T_c}{T_0} \right)
\end{equation}
%ENDLATEX%
where T0 is some parameter determining the steepness of the slope.
Or choosing to work in terms of resistance, we can solve for T in order to substitute it into the { P , R , T } relation.
%BEGINLATEX%
\[
T = T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right)
\]
%ENDLATEX%
Substituting:
%BEGINLATEX%
\begin{equation}
\mathrm{Low Pass} \left( P_{sky} + \frac{V_{bias}^2}{R} \right) = G \left[T_c + T_0 \mathrm{tan}\left( \pi \left[ \frac{R}{1 \Omega} - \frac{1}{2} \right] \right) \right]
\end{equation}
%ENDLATEX%
This equation has no closed form for R. Two options are:
- Use a root finder to solve the equation for R at each timestep.
- Approximate the transition by a linear function (Taylor expansion about an assumed stable point) and solve for R analytically.
Parameters: First TES Simulation
I used order 1 parameters for frequencies, voltages and power values to avoid numerical issues. The transition used is the arctan function with Tc=0.05, Tc=1 such that the maximal alpha=40 occurs at R=0.5 and T=Tc=1.
Results
The Simulink simulation looks as follows: where the "Scope" looks at the bolometer resistance. Varying the strength of the sky signal results in the following plots.
where the "Scope" looks at the bolometer resistance. Varying the strength of the sky signal results in the following plots.


 So the bias voltage is keeping the TES at R >= 0.5 and the sky signal can linearly alter the resistance up to R >> 0.5 where the TES saturates at R = 1.
So the bias voltage is keeping the TES at R >= 0.5 and the sky signal can linearly alter the resistance up to R >> 0.5 where the TES saturates at R = 1.
Bolo I-V curve
The current as a function of carrier voltage amplitude is shown in the following plot. The axes should be:- X axis: Carrier Voltage (V)
- Y axis: Current (A)
 Note the inverse relation between I-V at low voltages, the turnaround and the linear behaviour when the bolometer resistance saturates at 1 Ohm. At the lowest voltages, the input impedance of the current meter takes over and the relation becomes linear at a resistance of 0.1 Ohm + Rbolo ( T = 0 )
The feature at the high V end of the plot is an artifact (from when I started the simulation).
Note the inverse relation between I-V at low voltages, the turnaround and the linear behaviour when the bolometer resistance saturates at 1 Ohm. At the lowest voltages, the input impedance of the current meter takes over and the relation becomes linear at a resistance of 0.1 Ohm + Rbolo ( T = 0 )
The feature at the high V end of the plot is an artifact (from when I started the simulation).
Amplifier Input Impedence
The input impedence of the amplifier is a non-ideality. The above I-V curve has Rinput = 0.1 Ohm. The following I-V curves have Rinput = 0.2 Ohm (top) and Rinput = 0.4 Ohm (bottom).
 The I_*_V = const part of the curve is the interesting part, since that is where the power applied to the bolometer is constant. For large input impedances, the curve deviates from I_*_V = const behaviour. That deviation implies deviation from strong electrothermal feedback.
-Tijmen
The I_*_V = const part of the curve is the interesting part, since that is where the power applied to the bolometer is constant. For large input impedances, the curve deviates from I_*_V = const behaviour. That deviation implies deviation from strong electrothermal feedback.
-Tijmen
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
arctan.gif | manage | 8.2 K | 2009-05-08 - 14:30 | WinterlandUser | |
| |
bolo_iv.png | manage | 5.2 K | 2009-05-14 - 14:27 | WinterlandUser | |
| |
bolo_iv_0.2.png | manage | 5.2 K | 2009-05-14 - 17:24 | WinterlandUser | |
| |
bolo_iv_0.4.png | manage | 4.9 K | 2009-05-14 - 17:35 | WinterlandUser | |
| |
bolo_iv_new.png | manage | 5.2 K | 2009-05-14 - 15:43 | WinterlandUser | |
| |
high.png | manage | 12.0 K | 2009-05-11 - 15:35 | WinterlandUser | |
| |
medium.png | manage | 11.3 K | 2009-05-11 - 15:33 | WinterlandUser | |
| |
none.png | manage | 10.9 K | 2009-05-11 - 15:33 | WinterlandUser | |
| |
success2.png | manage | 17.6 K | 2009-05-11 - 15:21 | WinterlandUser | |
| |
trans2.png | manage | 6.0 K | 2009-05-11 - 15:17 | WinterlandUser |
This topic: ColdFeedback > WebHome > StrongElectrothermalFeedback Topic revision: r9 - 2011-11-17 - TijmenDeHaan
© 2020 Winterland Cosmology Lab, McGill University, Montréal, Québec, Canada

